首先简单说明一下ORB-SLAM的变量名前缀设计：
以单目情况 mono_tum.cc 为例，调用 LoadImages 函数加载图片和时间戳后开始创建SLAM系统，用于初始化所有系统线程（Local Mapping、Loop Closing、Viewer）并为下一步处理帧做准备。
本类定义在 System.h 中，实现在 System.cc 中。构造函数定义如下
1 | System(const string &strVocFile, //指定ORB字典文件的路径 |
其中，eSensor 是一个枚举类型，用于表示本系统所使用的所有传感器类型
八叉树是一种树形数据结构，每个节点有0个或8个子节点，常用于分割三维空间，因为一个正方体最少可以等分为八个小正方体。在3D物体建模中是一种非常有效的存储数据的方法，尤其对于流形物体、点云图、体素这类稀疏化（sparse）数据而言，八叉树可以更好地展现数据的结构特性。
将一个物体用最小的立方体包裹起来，然后对这个立方体使用八叉树的方式进行分割。因为是立体空间，所以每次划分都会把一个方块分为8个等分的子方块，若某个子方块中没有包含这个物体，那么就把这个小方块储存的数据置为0，表示这是一个空的区域；反之置为1，并继续分割下去，直到不存在部分被物体占据的子方块后停止分割（要么不包含该物体，要么被该物体占满）。
第一次分割完后只有两个方块非空，于是这两个位置的数据被置为1，其他全为0；然后继续分割值为1的子方块，直到达到最大深度后停止分割。如图所示，最终需要用1+8+64=73位（bit）来存储这种八叉树结构：1 01010000 00000000 01010000 00000000 01010000… 第一位的数字1表示根节点，第二位到第九位数字01010000表示了八叉树分割深度达到2时的子节点的分割情况，以此类推，深度为3时一共需要8*8=64位来储存相应的子节点的分割情况。
因此，为了看清楚物体的形状，只需要找到这73个位置对应的数值就行了。而对于同样的分辨率的体素来说，因为是3维空间，每一点都有3个坐标，所以建立同样的空间我们需要多达8*8*8=512个点的坐标索引，因此也就需要记录512个位置的数据。这种思想叫做位表示（Bit-representation），它能帮助我们更加高效地存储稀疏化数据。
八叉树数据结构可以更高效地储存数据，减少计算机内存和磁盘空间的占用，这一特点使得其在3D模型等稀疏化数据处理中逐渐受到学者的青睐。同时八叉树也是一种对数据的特征提取，因为八叉树一层一层不断划分子空间的过程也包含了物体的空间信息，这也给我们后续的数据进一步处理（比如说计算机视觉领域的物体分类等）提供了便利。
octree模块提供了对 octree 数据结构的实现，利用FLANN进行快速邻域检索，邻域检索在匹配、特征描述子计算、邻域特征提取中是非常基础的核心操作。octree 模块包含 17 个类，实现对点云的高效管理和检索以及相应的一些空间处理算法，例如压缩、空间变化检测等，依赖于 pcl_common 模块。
pcl::octree::Octree2BufBase<LeafContainerT, BranchContainerT>kd-tree概念的基本介绍可以参考这篇博客
PCL中的kd-tree库提供了kd-tree数据结构，基于FLANN进行快速最近邻检索。最近邻检索在匹配、特征描述子计算、邻域特征提取中是非常基础的核心操作。
kd-tree模块包括了三个类和两个函数，实现了利用kd-tree数据结构对点云进行高效管理和检索，依赖于 pcl_common 模块。
三个类的继承关系如图：
KdTree类实现了kd-tree的数据结构，关键成员函数如下：
1 | KdTree(bool sorted=true); // 空的构造函数 |
virtual int nearestKSearch 纯虚函数，共有三种形式，具体实现在子类 KdTreeFLANN 中，用来进行K邻域搜索。
（1）根据提供的点云和待查询点的索引进行搜索
1 | virtual int pcl::KdTree< PointT >::nearestKSearch( |
[input] cloud：点云数据
[input] index：所查询点的索引（必须是有效的索引，该函数不会对有效性进行检查）
[input] k：K邻域个数
[output] k_indices：搜索完的邻域点对应的索引
[output] k_sqr_distances：搜索完的每个邻域点与查询点之间的欧氏距离
返回找到的邻域点个数
（2）根据提供的待查询点进行搜索
1 | virtual int pcl::KdTree< PointT >::nearestKSearch( |
[input] p_q：待查询点
其他与上同
（3）根据提供的待查询点索引进行搜索
1 | virtual int pcl::KdTree< PointT >::nearestKSearch( |
virtual int radiusSearch 纯虚函数，类似nearestKSearch，共有三种形式，具体实现在子类 KdTreeFLANN 中，用来进行r半径内的邻域搜索。
（1）根据提供的点云和待查询点的索引进行搜索
1 | virtual int pcl::KdTree< PointT >::radiusSearch( |
[input] radius：搜索半径
[input] max_nn：设置返回的邻域点个数商店，若为0或大于返回邻域点个数，则返回全部搜索结果
其他与上同，返回半径内搜索到的邻域点个数
（2）根据提供的待查询点进行搜索
1 | virtual int pcl::KdTree< PointT >::radiusSearch( |
（3）根据提供的待查询点索引进行搜索
1 | virtual int pcl::KdTree< PointT >::radiusSearch( |
基本与上无差别，具体参见官方手册
void pcl::getApproximateIndices
获取参考点云中查询点云的近似索引向量（两个点云的坐标类型可以不同）
1 | template<typename PointT> |
[input] cloud_in：待查询点云的引用
[input] cloud_ref：参考点云的引用
[output] indices：返回查询结果在参考点云中的索引向量
运行输出：
OpenNI是一个多语言、跨平台的框架，主要目的是形成标准的、用于<视音频传感器>和<视音频感知中间件>间通信的API，兼容设备包括Primesense Reference Design、Microsoft Kinect 和 Asus XtionPro三种摄像头设备
包括有21个类和28个函数，实现对点云的获取、读入、存储等操作，既可通过点云文件进行输入输出，也可以通过封装借口直接从兼容设备获取源数据（包括RGB图像、深度图像和红外图像）。依赖 pcl_common 和 pcl_octree 及 OpenNI 外部开发包。
每个PCD文件都有一个文件头用来声明文件中存储的点云数据的各项特性，文件头必须用ASCII码编码，从0.7版本开始文件头按顺序包含以下字段，各字段之间用换行隔开：
VERSION：指定PCD文件版本
FIELDS：指定一个点可以有的每个维度和字段的名字
1 | FIELDS x y z # XYZ 坐标数据 |
SIZE：用字节数指定每个维度的大小
1 | unsigned char / char -> 1 byte |
TYPE：用一个字符指定每个维度的类型
I ：表示有符号类型U ：表示无符号类型F ：表示浮点类型COUNT：指定每个维度包含的元素数目（实际上是在给每个点引入n维直方图描述符的方法）默认情况下所有维度数目为1
WIDTH：用点的数量表示点云数据集的宽度
HEIGHT：用点的数量表示点云数据集的高度（用来检查一个点云数据集是否有序）
VIEWPOINT：指定数据集中点云的获取视点，视点信息被指定为 平移（tx ty tz) + 四元数（qw qx qy qz），默认值为 VIEWPOINT 0 0 0 1 0 0 0
POINTS：指定点云中点的总数
DATA：指定存储点云数据的数据类型，包括ASCII码和二进制两种。DATA的下一个字节开始就被视为点云的数据部分
举例
1 | # .PCD v.7 - Point CLoud Data file format |
这是一个0.7版本的PCD文件，每个点都有一个三维坐标数据和一个rgb颜色数据，四个维度均以浮点4字节存储（即float类型变量）。点云数据集无序，共213个点，默认视角，数据以ASCII码格式存储。
1 | int pcl::io::loadPCDFile<PointT> ( |
返回-1表示读取失败
1 | int pcl::io::savePCDFileASCII ( |
点连接：即将两个格式相同（包括字段类型和维度都要相同）的点云中的点合并。<增加点数>
1 | cloud_c = cloud_a; |
输出：
-IO模块/1626140895249.png)
域（字段）连接：例如点云A为N个点的XYZ点（pcl::PointXYZ），点云B为N个点的法向量（pcl::Normal），那么将两个点云进行字段连接得到的点云C则为N个点的pcl::PointNormal类型。<增加维度>
1 | void pcl::concatenateFields ( |
例：
1 | pcl::concatenateFields(cloud_a, n_cloud_b, p_n_cloud_c); |
输出：
给Ubuntu装PCL是大二时候的事情了，那时候在自己电脑的双系统上装，root权限和网络都有，apt-get安装非常快。现在开始学PCL库，在实验室服务器上重新来装一遍，不同的是，这次既没有root权限也没有网页，就会麻烦很多，折腾了一天，记录一下。
PCL需要的依赖库有点多，包括：
如果有root权限不妨选择全部都装一遍：
1 | sudo apt-get update |
关于Boost库的版本问题，由于我的系统是Ubuntu16.04，只支持到1.58，所以只能apt安装1.7版本的PCL；如果从源码安装更高版本的PCL则需要另外安装更高版本的Boost库。
接着：
1 | sudo apt-get install libpcl-dev |
这样子PCL就安装完成啦！
因为没有root权限，所以apt-get是用不了了，服务器没连网，所以git/wget也用不了，所有依赖库需要从 Ubuntu Package 网站上下载对应源码包，用ftp传到服务器上进行源码安装。比较麻烦，就只安装了必需的四个库。
需要注意的是，在编译安装前需要根据 Ubuntu Package 提供的依赖库进行检查，例如 libxt-dev 的依赖库有以下：
使用 dpkg -s 库名称 检查服务器上是否已经安装过需要的依赖库，如果没有，就需要自己一个一个手动下载编译安装。如果嫌一个个检查麻烦的话，也可以直接安装四个依赖库，根据报错去补依赖库（没错就是我）。以openmpi为例介绍如何将依赖库安装到非root用户目录下。
首先开一个新的文件夹存放下载的源码文件（例如我的：~/Download），再开一个文件夹仿照 /usr 存放安装的各种头文件、链接库等等文件（例如我的：~/Software）。
主机下载完openmpi源码后ftp上传到服务器，会发现这一类源代码没有熟悉的CMakeLists而是直接的Makefile。
根据我们之前设置的安装路径进行config：
1 | ./configure --prerfix=/home/panweihong/Software |
这里的prefix就是将来这个库会被安装在哪个目录底下，默认是 /usr ，显然我们没有操作 /usr 目录的权限，所以需要把它改成我们自己的安装目录，并且需要特别注意的是，这里写的必须是绝对路径，像 ~/Software 这样子是不行的。
config没有问题后就可以开始编译安装了：
1 | make -j8 && make install -j8 |
能开多核就开多核，速度能提快不止一点点。没有报错就okk；有报错大概率就是依赖库的问题，检查一下缺了什么库，再针对性地安装即可，安装过程和这个一模一样。
不过这样还没有完全结束，因为是手动安装，所以也需要手动配置路径。打开 ~/.bashrc 文件，添加：
1 | export LD_LIBRARY_PATH=/你的安装目录/lib:$LD_LIBRARY_PATH |
$VAR ：表示引用 VAR 这个变量的值各路径由 : 隔开，设置好后退出 ~/.bashrc 并 source ~/.bashrc 后，在终端执行 echo $某个变量名 检查是否生效。
另外一个小问题，因为每次 source ~/.bashrc 后文件中的 export 语句都会被执行一次，导致路径中有很多重复值，我的解决方法比较笨。就是在第一次export自己的路径前先echo一下这个变量原来的默认值，然后直接复制到原来 $变量 的位置，这样就不会因为重复export重复引用路径导致出现很多重复值了，这么做的原因是每次source的时候都会在第一个export给这个变量重新赋值，之后再有export就不会重复之前的值了，所以，后面再次export这个变量就和之前一样写 $变量明 就行了。
本来boost库服务器上已经安装好了，我之所以重新安装，是因为最后编译PCL库的时候报了这个错：
这两个库其实都是有的，用 locate 命令都能找得到，但就是多了个后缀：
1 | /usr/lib/x86_64-linux-gnu/libboost_system.so.1.65.1 |
本来是一个建立软链接就能解决的小事：
1 | cd /usr/lib/x86_64-linux-gnu/ |
但尴尬的是，没有权限啊！！！所以只能自己重新安装了Orz
先去 sourceforge 下载自己需要版本的boost源码，在解压文件夹下执行：
1 | ./bootstrap.sh --prefix=/home/panweihong/Software |
如果系统中已经有了预装的boost，为了让自己的boost库能被找到，在cmake的时候加上编译条件 -DBOOST_ROOT=/你的安装目录 ，例如我就是 -DBOOST_ROOT=/home/panweihong/Software
先去 Eigen官网 下载自己需要版本的Eigen源码，在解压文件夹下执行：
1 | mkdir build |
同样先下载 FLANN源码 ，在解压文件夹下执行与Eigen3安装相同的操作。
我遇到了一个非常神奇的问题，在用 3.15版本的cmake编译时，出现了这样的错误：
参考这个解决方法 ，我重装了一个 3.10版本的cmake（从这里下源码，tar.gz文件不用安装，解压后直接添加环境变量就能用），再次编译就没有这个问题了（震惊.jpg）
这是折腾了我最久的依赖库Orz
首先下载需要的源码文件：VTK-8.2.0.tar.gz和VTKData-8.2.0.tar.gz，将VTKData解压到VTK文件下，执行与Eigen3安装类似的操作。
1 | mkdir build |
libxt-dev cmake的时候报错：
1 | X11_Xt_LIB could not be found. Required for VTK X lib. |
这是缺少 libxt_dev ，去 Ubuntu Package 上下载源码包，又缺依赖 libsm-dev ，libsm-dev 又缺 libice-dev （禁止套娃）。都下载编译安装，方法和上面讲的openmpi一样。不过在make的时候报了这样一个错误：
1 | cc: error: ./sepces: Is a directory |
参考这个解决方法，LD_LIBRARY、LPATH 和 GCC_EXEC_PREFIX 不能以 : 开头或结尾，并且泵你在中间的任何地方包含 :: ，而像这种方法：
1 | export VAR=some/new/path:$VAR |
就很容易导致上述问题（当变量初始值为空时）。所以需要在 ~/.bashrc 末尾添加一行用来删除路径中的空值：
1 | LD_LIBRARY_PATH=$(echo $LD_LIBRARY_PATH | sed -E -e 's/^:*//' -e 's/:*$//' -e 's/:+/:/g') |
VTK在进行make的时候会下载一些测试数据到build的ExternalData文件夹下，但由于服务器断网，所以会出现 (Couldn't connect to server) 的问题。因为我在自己的双系统上安装过，所以还保留了下载完成的ExternalData文件夹，将该文件夹复制到build文件夹下，再执行make操作就不会报错了。这个数据文件我上传到百度云，提取码为64gw，我的VTK是8.2.0版本。
下载源码文件 ，在解压文件夹下执行类似操作：
1 | mkdir build |
从官网上拷贝了一份代码下来
1 |
|
CMakeLists.txt如下：
1 | cmake_minimum_required(VERSION 2.6 FATAL_ERROR) |
如果和我一样在vscode里跑的话，在c_cpp_properties.json文件中的includePath加入PCL和Eigen3（如果需要）的头文件路径后就不会报头文件找不到的错误了
1 | "/home/panweihong/Software/include/pcl-1.9", |
执行 ./pcd_write_test 输出：
1 | Saved 5 data points to test_pcd.pcd |
成功输出就说明安装成功了！
域 $\mathbb{R}$ 上的集合 $\mathbb{V}$ 对向量加法(vector summation)和数乘(scalar multiplication)封闭
即：$\forall \boldsymbol{v_1},\boldsymbol{v_2}\in\mathbb{V},\forall \alpha,\beta\in\mathbb{R}, \alpha\boldsymbol{v_1}+\beta\boldsymbol{v_2}\in\mathbb{V}$
加法和数乘具体定义和满足的条件见矩阵分析第一讲
$\mathbb{W}\subset\mathbb{V},\boldsymbol{0}\in\mathbb{W}$，且对加法和数乘封闭，则称 $\mathbb{W}$ 为向量空间 $\mathbb{V}$ 的子空间
一组向量 $\mathbb{S}=\{\boldsymbol{v_1},…,\boldsymbol{v_k}\}\subset\mathbb{V}$ 的生成子空间定义为：
集合 $\mathbb{S}$ 线性无关的条件：
即集合中的所有向量都不能被其他向量所表示，反之则称该集合线性相关
向量组 $\mathbb{B}=\{\boldsymbol{v_1},…\boldsymbol{v_n}\}$ 线性无关且生成子空间为 $\mathbb{V}$ ，则称向量组 $\mathbb{B}$ 为线性空间 $\mathbb{V}$ 的一组基，即线性无关向量的最大集合
若向量组 $\mathbb{B}$ 和 $\mathbb{B’}$ 是线性空间 $\mathbb{V}$ 的两组基，那么有以下三个结论
$\mathbb{B}$ 和 $\mathbb{B’}$ 中的向量个数相等，均为 $n$ ，称为线性空间 $\mathbb{V}$ 的维度
$\forall \boldsymbol{v}\in\mathbb{V}$ 都可由向量组 $\mathbb{B}$ 中的基向量唯一线性表出
特殊地，向量组 $\mathbb{B’}$ 中的所有向量都可由 $\mathbb{B}$ 线性表出：
该基变换中的系数 $a_{ji}$ 组成矩阵 $\boldsymbol{A}$，$\boldsymbol{B}=[b_1,…b_n],\boldsymbol{B’}=[b_1’…,b_n’]$ ，故上式可写作：
内积(Inner Product)
在向量空间中定义内积（点积）$\langle\cdot,\cdot\rangle:\mathbb{V}\times\mathbb{V}\rightarrow\mathbb{R}$ ，满足以下三个条件：
从而定义了一个范数(norm) ：
和一个度量(metric) ：
分别用来计算向量长度和向量间的距离，这使得 $\mathbb{V}$ 成为一个度量空间，又因为该度量是由向量内积定义的，所以又称 $\mathbb{V}$ 为希尔伯特空间(Hilbert Space)
标准内积与生成内积(Canonical Inner Product and Induced Inner Product)
特殊地，在 $\mathbb{V}=\mathbb{R}$ 时，可以由标准基 $\boldsymbol{B}=\boldsymbol{I}_n$ (n维单位矩阵)定义标准内积：$\langle \boldsymbol{x},\boldsymbol{y}\rangle=\boldsymbol{x}^T\boldsymbol{y}=\sum^n_{i=1}x_iy_i$ ，从而定义出了标准 $L_2$ 范数（欧几里得范数）$|\boldsymbol{x}|=\sqrt{\boldsymbol{x}^T\boldsymbol{x}}=\sqrt{x_1^2+…+x_n^2}$
对于一个新给出的基底 $\boldsymbol{B}’$ ，有基变换 $\boldsymbol{A}$ 使得 $\boldsymbol{I}=\boldsymbol{B}’\boldsymbol{A}^{-1}$ ，那么标准内积用新坐标 $\boldsymbol{x}’,\boldsymbol{y}’$ 可表示为：$\langle\boldsymbol{x},\boldsymbol{y}\rangle=\boldsymbol{x}^T\boldsymbol{y}=(\boldsymbol{Ax}’)^T(\boldsymbol{Ay}’)=\boldsymbol{x}’^T\boldsymbol{A}^T\boldsymbol{A}\boldsymbol{y}’\equiv\langle\boldsymbol{x}’,\boldsymbol{y}’\rangle_{\boldsymbol{A}^T\boldsymbol{A}}$ ，后者成为变换矩阵 $\boldsymbol{A}$ 下的生成内积
当且仅当 $\langle\boldsymbol{v},\boldsymbol{w}\rangle=0$ 时向量正交
(新概念) 矩阵的 Kronecker积 和 Stack（堆）
给定两个任意大小的矩阵 $\boldsymbol{A}\in\mathbb{R}^{m\times n}$ 和 $\boldsymbol{B}\in\mathbb{R}^{k\times l}$ ，定义它们的 Kronecker积 如下：
矩阵 $\boldsymbol{A}$ 的 Stack (堆) $\boldsymbol{A}^s$ 则定义为一个由所有n个列向量纵向堆叠而成的的列向量：
上述定义使得代数表达式可以被重写得更加直观，例如：
这其实是容易证明的：
线性代数研究的是两个线性空间之间的线性变换，由于这些线性变换都可以用矩阵表示，所以线性代数相当于在研究矩阵的特性。
两个线性空间 $\mathbb{V}$ 和 $\mathbb{W}$ 之间的 线性变换(Linear Transformation) 是一个映射 $\boldsymbol{L}: \mathbb{V}\rightarrow\mathbb{W}$ ，它满足以下两个条件：
由于线性性，线性变换 $\boldsymbol{L}$ 对空间 $\mathbb{V}$ 的操作可以唯一定义为对 $\mathbb{V}$ 上基向量的操作，对标准基 $\{\boldsymbol{\theta_1},…,\boldsymbol{\theta_n}\}$ 有：$\boldsymbol{L}(\boldsymbol{x})=\boldsymbol{Ax}\quad \forall\boldsymbol{x}\in\mathbb{V}$ 其中 $\boldsymbol{A}=(\boldsymbol{L}(\boldsymbol{\theta_1}),…,\boldsymbol{L}(\boldsymbol{\theta_n}))\in\mathbb{R}^{m\times n}$
所有 $m\times n$ 维实矩阵组成的集合记为 $\mathcal{M}(m,n)$ ，当 $m=n$ 时，集合 $\mathcal{M}(m,n)\equiv\mathcal{M}(n)$ 就形成了域 $\mathbb{R}$ 上的一个 环，即满足对矩阵乘法和矩阵加法封闭
线性群 $GL(n)$ 和 $SL(n)$
群 的概念：集合 $\mathbb{G}$ 与集合 $\mathbb{G}$ 上定义的一种运算：$\circ :\mathbb{G}\times\mathbb{G}\rightarrow\mathbb{G}$ 满足以下四个条件：
这样的集合就称为群 。
一个群 $G$ 有矩阵表示（可被视为矩阵群）的条件：
该映射保留了群 $G$ 的群结构，即保留了幺元、群乘、可逆性等：
之所以引进群的矩阵表示，是因为这能实现从研究矩阵群的特征角度来研究更抽象的群。
例如：物体旋转运动构成了一个群，如果能用矩阵表示旋转，那么研究旋转群的特征会容易很多
仿射群 $A(n)$
仿射变换 $L:\mathbb{R}^n\rightarrow \mathbb{R}^n$ 可以由一个矩阵 $\boldsymbol{A}\in GL(n)$ 和一个向量 $\boldsymbol{b}\in \mathbb{R}^n$ 唯一定义 ：
由这些仿射变换构成的集合称为 $n$ 维仿射群 ，记作 $A(n)$
显然，上述定义的仿射变换 $L$ 不是个线性映射，除非 $\boldsymbol{b}=\boldsymbol{0}$。通过引入 齐次坐标 （将 $\boldsymbol{x}\in\mathbb{R}^n$ 表示为 $\left(\begin{matrix}\boldsymbol{x}\\1\end{matrix}\right)\in\mathbb{R}^{n+1}$ ）可以把 $L:\mathbb{R}^n\rightarrow \mathbb{R}^n$ 变成一个线性映射 $L:\mathbb{R}^{n+1}\rightarrow \mathbb{R}^{n+1}$ ：
矩阵 $\left(
\begin{matrix}
\boldsymbol{A} \quad \boldsymbol{b} \\
\boldsymbol{0} \quad\ 1
\end{matrix}
\right)\in GL(n+1)$ 称为 仿射矩阵 ，所有仿射矩阵构成了 $GL(n+1)$ 的一个子群
正交群 $O(n)$
所有 $n\times n$ 的正交矩阵构成了正交群 $O(n)=\{\boldsymbol{R}\in GL(n)|\boldsymbol{R}^T\boldsymbol{R}=\boldsymbol{I}\}$ ，显然它是群 $GL(n)$ 的子群，且 $\text{det}(\boldsymbol{R}^T\boldsymbol{R})=(\text{det}(\boldsymbol{R}))^2=\text{det}(\boldsymbol{I})=1\Rightarrow\text{det}(\boldsymbol{R})\in\{+1,-1\}$
将 $O(n)$ 满足 $\text{det}(\boldsymbol{R})=+1$ 的子群称为 特殊正交群 ，记作 $SO(n)$ ，显然 $SO(n)=O(n)\cap SL(n)$ 。特别地，$SO(3)$ 即为三维旋转矩阵构成的群（行列式为-1的矩阵为镜像矩阵）
欧氏群 $E(n)$
由正交阵 $\boldsymbol{R}\in O(n)$ 和向量 $\boldsymbol{T}\in \mathbb{R}^n$ 定义出一个欧氏变换：$L:\mathbb{R}^n\rightarrow \mathbb{R}^n;\quad \boldsymbol{x}\mapsto\boldsymbol{Rx+T}$
由这种变换组成的集合称为欧几里得群（欧氏群）$E(n)$ ，显然它是仿射群 $A(n)$ 的子群，基于齐次坐标，欧氏群的矩阵表示如下：
对应地，若 $\boldsymbol{R}\in SO(n)$ ，那么此时的欧氏群称作 特殊欧氏群 ，记作 $SE(n)$ 。特别地，$SE(3)$ 表示的是三维刚体运动。
综上，几个群之间的关系有：
设 $\mathbb{V}$ 是 $\mathbb{R}$ 上的一个线性空间，定义映射 $\tau: \mathbb{V}\times\mathbb{V}\rightarrow\mathbb{R}$ 。称映射 $\tau$ 为 $\mathbb{V}$ 上的一个内积，且记 $\tau(v_1,v_2)=
(1) 对称性: $
(2) 固定第一个变元，对第二个变元有线性性: $
(3) 正定性: 对 $\forall v\neq0,
定义了内积的线性空间称为内积空间，有限维的内积空间称为欧几里得空间（有限维内积空间）
内积有如下性质：
(1) $<\boldsymbol{0},\boldsymbol{v}>=0$
(2) 双线性：固定第二个变元，对第一个变元也满足线性性
定义映射 $\tau: \mathbb{R}^n\times\mathbb{R}^n\rightarrow\mathbb{R}$ ，满足 $<\boldsymbol{x},\boldsymbol{y}>=\boldsymbol{x}^T\boldsymbol{y}=x_1y_1+x_2y_2+…+x_ny_n$ ，称 $\tau$ 为 $\mathbb{R}^n$ 上的标准内积
为了解决数域矩阵相似最简型的问题，我们引入 $\lambda$ 矩阵
以多项式为元素的矩阵
$\lambda$ 矩阵的秩
单位模阵：逆矩阵，且必须是多项式矩阵，因为单纯逆矩阵 $\boldsymbol{A}^{-1}=\frac{1}{|\boldsymbol{A}|}\boldsymbol{A}^*$ 不一定是多项式矩阵
多项式矩阵相对于前面所谈论的数值矩阵，主要不同就在于除法运算上，即多项式相除结果不一定还是多项式。用抽象数学的概念，数值矩阵谈论是域上的矩阵，而多项式矩阵谈论的是环上的矩阵
下面给出证明：
$\Leftarrow$ ：显然
$\Rightarrow$ ：存在多项式矩阵 $\boldsymbol{V}(\lambda)$ ，使得 $\boldsymbol{U}(\lambda)\boldsymbol{V}(\lambda)=\boldsymbol{I}_n\Rightarrow|\boldsymbol{U}(\lambda)||\boldsymbol{V}(\lambda)|=1\Rightarrow f(\lambda)g(\lambda)=1$ ，两个多项式相乘等于1，这两个多项式只能是 $a_0\neq 0$ 的零次多项式，否则相乘一定有变量在
以初等行变换为例 $\Leftrightarrow$ 左乘一个相应的初等矩阵：
某两行互换 $\Leftrightarrow$ eg. $\begin{bmatrix} 0&1&0\\1&0&0\\0&0&1\end{bmatrix}$
某行乘以非零常数 $\Leftrightarrow$ eg. $\begin{bmatrix} c&0&0\\0&1&0\\0&0&1\end{bmatrix}$
注：不是乘以非零多项式！因为乘以多项式是不可逆的，即对应乘上的矩阵没有单位模阵
某行乘以一个多项式再加到另一行上 $\Leftrightarrow$ eg. $\begin{bmatrix}1&0&0\\f(\lambda)&1&0\\0&0&1\end{bmatrix}$
$\lambda$ 矩阵的等价：经初等行列变换可以互相转化的两个 $\lambda$ 矩阵等价，记作 $\boldsymbol{A}(\lambda) \sim \boldsymbol{B}(\lambda) $
【用初等行变换为矩阵左上角降次】设 $\boldsymbol{A}(\lambda) =[a_{ij}(\lambda)]_{m\times n},\ a_{11}(\lambda)\neq0$ ， 且至少有一个元素不能被 $a_{11}(\lambda)$ 整除（$\Leftrightarrow a_{11}(\lambda)$ 不为非零常值多项式 ），则有 $\boldsymbol{A}(\lambda) \sim\boldsymbol{B}(\lambda) $ 且 $b_{11}(\lambda)\neq0,\ \partial(b_{11}(\lambda))<\partial(a_{11}(\lambda))$ （$\partial(多项式)$ 表示该多项式的次数）
下面给出证明概要：
同行中有一个元素 $a_{1j}(\lambda)$ 不能被 $a_{11}(\lambda)$ 整除，即 $a_{1j}(\lambda)=a_{11}(\lambda)q(\lambda)+r(\lambda),\ 且\ \partial(r(\lambda))<\partial(a(\lambda))$ ，所以，将第一列乘以 $-q(\lambda)$ 加到第 $j$ 列后交换第一列与第 $j$ 列，此时 $a_{11}(\lambda)’=r(\lambda),\partial(a_{11}(\lambda)’)<\partial(a_{11}(\lambda))$ ，从而实现降次
同列中有一个元素 $a_{i1}(\lambda)$ 不能被 $a_{11}(\lambda)$ 整除，同理
同行同列都能被整除，但有 $a_{ij}(\lambda)$ 不能被 $a_{11}(\lambda)$ 整除。
首先可以通过一系列行列变换把第一列、第一行除了 $a_{11}(\lambda)$ 外都化为0，同时保证变换后的 $a_{ij}(\lambda)’$ 仍旧不能被 $a_{11}(\lambda)$ 整除（不能被整除的数加上除数的倍数依然不能被整除），将变换后的第 $j$ 行加到第1行，就回到第一种情况了
设：
其中 $r=\text{rank}(\boldsymbol{A}(\lambda))$ ，$d_i(\lambda)$ 为非零多项式，且 $d_i(\lambda)|d_{i+1}(\lambda)$ （$f(\lambda)|g(\lambda)$ 表示 $f$ 整除 $g$ ），则称 $\boldsymbol{B}(\lambda)$ 为 $\boldsymbol{A}(\lambda)$ 的 Smith标准型 。
下面给出证明：
存在性
若为零矩阵，则显然；若为非零矩阵，必存在非零多项式，通过行列变换将次数最低的非零多项式移到 $a_{11}(\lambda)$ ，会出现以下两种情况：
对于第二种情况，【用初等行变换为左上角降次】，降次必然是有限的，不能再降次的时候，也就是矩阵中的所有元素都能被 $a_{11}(\lambda)$ 整除的时候 ，进而同行同列的元素都能化成0
对右下子矩阵进行相同的操作，以此类推，最终得到 Smith标准型
唯一性
约定 $d_i(\lambda)$ 都是首1多项式，即最高次数系数为1
$\lambda$ 矩阵的 $k$ 阶行列式因子 ：$\boldsymbol{A}(\lambda)$ 的所有 $k$ 阶子式的最高公因式
初等变换不改变 $k$ 阶行列式因子
下面给出证明：
设 $\mathscr{A}=\{\boldsymbol{A}\ 的\ k\ 阶子式\},\mathscr{B}=\{\boldsymbol{B}\ 的\ k\ 阶子式\}$ ，只需证 $\mathscr{A},\mathscr{B}$ 的最高公因式相同。
任取 $f(\lambda)\in\mathscr{B}$ ，考察它与 $\mathscr{A}$ 中多项式的关系，由于初等变换是三种基本变换的组合，所以只需分别对三种基本变换进行讨论即可：
某两行互换：只影响行列式的符号，因为约定了所有多项式都是首1多项式，所以这种变换对子式集合无影响，即 $\mathscr{A}=\mathscr{B}$ ，那么必有 $f(\lambda)\in\mathscr{A}$
某行乘以一个非零常数：同样，因为约定了所有多项式都是首1多项式，所以也不会有影响，即 $\mathscr{A}=\mathscr{B}$ ，那么必有 $f(\lambda)\in\mathscr{A}$
某行乘以一个多项式再加到另一行上。假设是第 $i$ 行乘以 $h(\lambda)$ 加到第 $j$ 行。那么：
如果 $f(\lambda)$ 没有取到第 $j$ 行，那么该子式不发生变化，即 $f(\lambda)\in\mathscr{A}$ ；
如果 $f(\lambda)$ 取到了第 $j$ 行：
如果同时取到了第 $i$ 行，那么该子式不发生变化，即 $f(\lambda)\in\mathscr{A}$
如果没有取到第 $i$ 行，显然 $f(\lambda)\notin\mathscr{A}$ ，但是可以将它对应的行列式拆分：
即：$f(\lambda)=g(\lambda)+w(\lambda)\cdot h(\lambda)$，其中 $g(\lambda),w(\lambda)\in\mathscr{A}$ ，所以 $\mathscr{A}$ 的公因式必整除 $f(\lambda)$
综上，$\mathscr{A}$ 的公因式必能整除 $\mathscr{B}$ 中的所有子式，由于初等变换可逆知，$\mathscr{B}$ 的公因式也必能整除 $\mathscr{A}$ 中的所有子式，从而二者的最高公因式相同
不变因子 $d_{i}(\lambda)$
记 $k$ 阶行列式因子为 $D_k(\lambda)$ ，初等变换不改变行列式因子，所以：
因此，称 $d_i(\lambda)$ 为不变因子（行列式因子唯一，所以 $d_i(\lambda)$ 一定唯一）
初等变换：找次数最低项，要么能整除，要么能降次（带余除法）
例：
计算所有行列式因子
同上例，有 $D_1(\lambda)=1,D_2(\lambda)=\lambda(\lambda+1),D_3=\lambda^2(\lambda+1)^3$ ，故而 $d_1(\lambda)=1, d_2(\lambda)=\lambda(\lambda+1),d_3(\lambda)=\lambda(\lambda+1)^2$
单位模阵的 Smith 型为单位矩阵
下面给出证明：
$\boldsymbol{U}(\lambda)$ 是单位模阵 $\Leftrightarrow |\boldsymbol{U}(\lambda)|=c\neq0$ （为非零常数）$\Leftrightarrow\boldsymbol{U}(\lambda)$ 的 $n$ 阶行列式因子为1，且 $r=\text{rank}(\boldsymbol{U})=n$
又：$D_n(\lambda)=D_1(\lambda)\frac{D_2(\lambda)}{D_1(\lambda)}\cdots\frac{D_n(\lambda)}{D_{n-1}(\lambda)}=d_1(\lambda)d_2(\lambda)\cdots d_n(\lambda)$
所以：$d_i(\lambda)=1$ ，证毕
据此，单位模阵经过若干次初等变换后可以变成单位矩阵，写成矩阵的形式即为：
初等矩阵的逆矩阵仍为初等矩阵，因此：
把一个受约束的相似问题【 $\boldsymbol{AP}=\boldsymbol{PB}$ 行列变换必须配套】转换成了一个不受约束的等价问题【 $\boldsymbol{U}(\lambda)(\lambda\boldsymbol{I}-\boldsymbol{A})\boldsymbol{V}(\lambda)=\lambda\boldsymbol{I}-\boldsymbol{B}$ 行列变换无需配套】
下面给出证明：
多项式矩阵的次数
若 $\boldsymbol{A}(\lambda) = A_0+A_1\lambda+A_2\lambda^2+\cdots+A_r\lambda^r,\ 且\ A_r\neq0$ ，则称 $\boldsymbol{A}(\lambda)$ 的次数为 $r$ ，记作 $\partial(\boldsymbol{A}(\lambda))=r$ 。特别地，零多项式矩阵的次数无意义。
多项式矩阵乘积的次数
$\boldsymbol{A}(\lambda)\boldsymbol{B}(\lambda)=\boldsymbol{C}(\lambda)$，且 $\boldsymbol{A}(\lambda) = A_0+A_1\lambda+\cdots+A_r\lambda^r$ ，若满足：
1）三个矩阵均非零（零矩阵的次数无意义）
2）$A_r\in \mathbb{F}^{m\times m}$ 可逆（保证 $\boldsymbol{C}(\lambda)$ 的最高次矩阵系数 $C_{r+s}(\lambda)=A_r(\lambda)B_s(\lambda)$ 非零）
那么 $\partial(\boldsymbol{C}(\lambda))=\partial(\boldsymbol{A}(\lambda))+\partial(\boldsymbol{B}(\lambda))$
多项式矩阵的带余除法（以左除为例）：
$\boldsymbol{A}(\lambda) = A_0+A_1\lambda+\cdots+A_r\lambda^r\in(\mathbb{F}[\lambda])^{m\times m}$ ，若满足 $A_r\in\mathbb{F}^{m\times m}$ 可逆，那么对非零矩阵 $\boldsymbol{B}(\lambda)\in(\mathbb{F}[\lambda])^{m\times n}$ ，存在唯一矩阵 $\boldsymbol{Q}(\lambda), \boldsymbol{R}(\lambda)$ ，使得：$\boldsymbol{B}(\lambda)=\boldsymbol{A}(\lambda)\boldsymbol{Q}(\lambda)+\boldsymbol{R}(\lambda)$ ，其中 $\boldsymbol{R}(\lambda)=\boldsymbol{0}$ 或 $\partial(\boldsymbol{R}(\lambda))<\partial(\boldsymbol{A}(\lambda))$
$\Rightarrow$ ：取 $\boldsymbol{U}(\lambda)=\boldsymbol{P}^{-1},\boldsymbol{V}(\lambda)=\boldsymbol{P}$ ，因为 $\boldsymbol{P}$ 可逆，故行列式为非零常数，满足单位模阵的要求
$\Leftarrow$ ：从 $\boldsymbol{U},\boldsymbol{V}$ 找 $\boldsymbol{P}$
根据多项式矩阵带余除法，因为 $\boldsymbol{I}$ 可逆，所以：
其中：$\boldsymbol{R}(\lambda)=\boldsymbol{0}$ ，或 $\partial(\boldsymbol{R}(\lambda))<\partial(\lambda\boldsymbol{I}-\boldsymbol{B})=1$ ，即 $\boldsymbol{R}(\lambda)=\boldsymbol{R}\in\mathbb{F}^{n\times n}$ 为常数矩阵。因此：
比较等式两端变量 $\lambda$ 的系数可知，$\boldsymbol{V}^{-1}(\lambda)-\boldsymbol{Q}(\lambda)(\lambda\boldsymbol{I}-\boldsymbol{A})$ 也是常数矩阵，记作 $\boldsymbol{S}$ ，故而：
且由 $\lambda$ 系数知：$\boldsymbol{R}=\boldsymbol{S}$ ，从而有 $\boldsymbol{RA}=\boldsymbol{BR}$ ，只需证 $\boldsymbol{R}$ 可逆即可
要证明可逆，我们期望找出一个矩阵 $\boldsymbol{P}$ ，使得 $\boldsymbol{RP}=\boldsymbol{I}$ .
考虑到 $\boldsymbol{R}$ 是由矩阵 $\boldsymbol{U}(\lambda)$ 对矩阵 $\lambda\boldsymbol{I}-\boldsymbol{B}$ 作带余除法所得，对应地，也可以有：
将方程 (7) (10) 代入 $\boldsymbol{U}(\lambda)\boldsymbol{U}^{-1}(\lambda)=\boldsymbol{I}$ ，整理得：
代入方程 (9) ，整理得：
比较方程 (12) 两边 $\lambda$ 系数知：$\boldsymbol{R}\widetilde{\boldsymbol{R}}=\boldsymbol{I}$ ，从而 $\boldsymbol{R}$ 可逆。
证毕。
因为 $|\lambda\boldsymbol{I}-\boldsymbol{A}|$ 的最高次项 $\lambda^n$ 的系数必为1，因此，$\lambda\boldsymbol{I}-\boldsymbol{A}$ 作为多项式矩阵的秩为 $n$ 。从而它的Smith型矩阵为：
因此：$d_1(\lambda)\cdots d_n(\lambda)=|\lambda\boldsymbol{I}-\boldsymbol{A}|\Rightarrow\partial(d_1(\lambda))+\cdots+\partial(d_n(\lambda))=n$ 。若某个 $d_i(\lambda)$ 的次数为 $n_i\neq1$ ，那么必将多出 $n_i-1$ 个常数不变因子，根据首1多项式的约定，这些不变因子最终都会化为1。因此上述Smith型矩阵进一步表示为：
其中，$\partial(h_i(\lambda))=n_i$ 。假设有 $p$ 个非常数不变因子，那么等于1的不变因子共有 $n-p$ 个，且满足 $n-p=(n_1-1)+\cdots+(n_p-1)$ ，因此将对角线上的元素按一个 $h_i(\lambda)$ ，$n_i-1$ 个1配对进行重组，Smith型矩阵等价于如下矩阵：
每一小块都是 $\begin{bmatrix} 1&&&\\&\ddots&&\\&&1&\\&&&h_i(\lambda)\end{bmatrix}_{n_i\times n_i}$
特征矩阵的初等因子组
初等因子指的是将特征矩阵的所有非常数不变因子在 $\mathbb{F}[\lambda]$ 中作质因式分解时出现的质因式的方幂。所有初等因子组成初等因子组（显然初等因子组中的某个初等因子可能重复出现）。
$h_i(\lambda)\xlongequal{质因式分解}w_1^{r_{i1}}(\lambda)\cdots w_j^{r_{ij}}(\lambda)$ ，则每个质因式的方幂 $w_j^{r_{ij}}(\lambda)$ 就是一个初等因子，所有方幂组成了特征矩阵的初等因子组。
（实数域中的质因式包括 $x-c$ 和 $x^2+bx+c,且\ b^2-4c<0$ 两种情况；复数域中的质因式只有 $x-c$ 一种情况）
初等因子组与不变因子（行列式因子、初等因子）互相唯一决定
由不变因子决定初等因子组：根据定义，显然
例：已知矩阵 $\boldsymbol{A}$ 的特征矩阵 $\lambda\boldsymbol{I}-\boldsymbol{A}$ 的 Smith型 为：$\begin{bmatrix}1&0&0\\0&(\lambda+1)^2&0\\0&0&\lambda(\lambda+1)^2\end{bmatrix}$
显然初等因子组为：$\{(\lambda+1)^2,\lambda, (\lambda+1)^2\}$
由初等因子组决定不变因子：
例：设 $\boldsymbol{A}\in\mathbb{C}^{8\times8}$ ，且初等因子组为：$\{\lambda,\lambda^2,\lambda,(\lambda+1)^2,(\lambda+1)^2\}$ ，求不变因子。
由于不变因子满足 $d_i(\lambda)|d_{i+1}(\lambda)$ 所以最后一个不变因子的次数应该最高且所有质因式都应出现，以此类推：
下面通过对非常数不变因子 $h_i(\lambda)$ 在复数域上作质因式分解，将上述（15）进一步化为一种更特殊的形式
显然有 $r_1+r_2+\cdots+r_k=n_i$ ，逆用初等因子分解，因为子矩阵 $\begin{bmatrix} 1&&&\\&\ddots&&\\&&1&\\&&&h_i(\lambda)\end{bmatrix}_{n_i\times n_i}$ 有上述 $k$ 个初等因子，所以可以等价于（有相同的初等因子组）：
若 $\boldsymbol{A},\boldsymbol{B}\in\mathbb{F}^{n\times n}$ ，则下列结论等价：
例：证明 $\boldsymbol{A}$ 与 $\boldsymbol{A}^T$ 相似
因为只提供了抽象矩阵，所以适用于具体形式的2/3/4/6方法都不容易处理，因此考虑行列式因子
因为 $(\lambda\boldsymbol{I}-\boldsymbol{A})^T=\lambda\boldsymbol{I}-\boldsymbol{A}^T$ ，而矩阵转置行列式不变，因此显然 $\lambda\boldsymbol{I}-\boldsymbol{A}$ 与 $\lambda\boldsymbol{I}-\boldsymbol{A}^T$ 有相同的行列式因子
以下均在复数域上考虑，因而质因式只有 $\lambda-c$ 一种类型。
综合上面所说，特征矩阵可以有如下等价：
其中：$(\lambda-c_i)^{r_i},i=1,…,q$ 是特征矩阵的初等因子组。
从而：$\boldsymbol{A}\longrightarrow\lambda\boldsymbol{I}-\boldsymbol{A}\sim\boldsymbol{J}(\lambda)\sim\lambda\boldsymbol{I}-\boldsymbol{J}\longleftarrow\boldsymbol{J}$ ，满足这个条件的矩阵都与 $\boldsymbol{A}$ 相似
我们要做的，就是求出其中最简单的矩阵，也就是相似最简型
进一步，这个问题又可以拆分成针对各个子块的类似的问题，即：求一个尽可能简单的矩阵 $\boldsymbol{J}_i\in\mathbb{C}^{r_i\times r_i}$ ，使得 $\lambda\boldsymbol{I}_{r_i}-\boldsymbol{J}_i\sim\boldsymbol{J}_i(\lambda)$
若当块：对角线元素全为 $c_1$ ，次对角线元素均为1的矩阵：
结论：若当块所对应特征矩阵的Simth型即满足 $\lambda\boldsymbol{I}_{r_i}-\boldsymbol{J}_i\sim\boldsymbol{J}_i(\lambda)$
下面给出证明（本质就是证明两个多项式矩阵等价） ：
由于左边的 $r_i-1$ 阶行列式中有一个是1（右上角子块），所以左边矩阵的 $r_i-1$ 阶最高公因式只能是1，即左边矩阵的 $r_i-1$ 阶行列式因子为1。
从而所有比它低阶的行列式因子也只能是1，因为 $D_{i-1}(\lambda)$ 必须整除 $D_{i}(\lambda)$ 。
而左侧行列式等于右侧行列式，即左侧 $r_i$ 阶行列式因子与右侧相同。
故而两边矩阵的任意阶行列式因子都相同，从而矩阵等价。
综上所述，有如下定理：
给定矩阵 $\boldsymbol{A}\in\mathbb{C}^{n\times n}$ ，其特征矩阵 $\lambda\boldsymbol{I}-\boldsymbol{A}$ 的初等因子组为：$(\lambda-c_1)^{r_1},\cdots,(\lambda-c_q)^{r_q}$ ，取
则 $\boldsymbol{A}$ 的相似最简型为：
而 $\boldsymbol{J}$ 就是矩阵 $\boldsymbol{A}$ 的 Jordan标准型
一个域是一个运算系统，包括一个集合和在集合上定义的两种运算（加法和乘法）且两种运算都满足一定的运算规则
常用域：有理数域 $\mathbb{Q}$ ，实数域 $\mathbb{R}$ ，复数域 $\mathbb{C}$
给定非空集合 $\mathbb{V}$ 和域 $\mathbb{F}$ ，若存在映射 $\sigma:\mathbb{V}\times \mathbb{V}\rightarrow \mathbb{V},(\boldsymbol{\alpha},\boldsymbol{\beta})\mapsto\sigma(\boldsymbol{\alpha},\boldsymbol{\beta})$ ，即对集合 $\mathbb{V}$ 中的任意元素 $\boldsymbol{\alpha},\boldsymbol{\beta}$ ，在集合 $\mathbb{V}$ 中都存在唯一元素 $\boldsymbol{\gamma}$ ，使得 $\boldsymbol{\gamma}=\boldsymbol{\alpha}+\boldsymbol{\beta}\in\mathbb{V}$，则称 $\sigma$ 为集合 $\mathbb{V}$ 上的加法 。
注：定义中的 $\times$ 是集合之间的乘法，称为卡氏积/笛卡尔积，指的是从两个集合中任取一个元素组成的所有有序元素对的集合：$\mathbb{S_1}\times\mathbb{S_2}=\{(a,b)|a\in\mathbb{S_1},b\in\mathbb{S_2}\}$
给定非空集合 $\mathbb{V}$ 和数域 $\mathbb{F}$ ，若存在映射 $\sigma:\mathbb{V}\times \mathbb{F}\rightarrow \mathbb{V},(\boldsymbol{\alpha},k)\mapsto\sigma(\boldsymbol{\alpha},k)$ ，即对集合 $\mathbb{V}$ 中的任意元素 $\boldsymbol{\alpha}$ 和数域 $\mathbb{F}$ 中的任意元素 $k$ ，在集合 $\mathbb{V}$ 中都存在唯一元素 $\boldsymbol{\gamma}$ ，使得 $\boldsymbol{\gamma}=\boldsymbol{\alpha}\cdot k\in\mathbb{V}$，则称 $\sigma$ 为集合 $\mathbb{V}$ 上的数乘 。
若集合 $\mathbb{V}$ 满足上述两种运算，且这两种运算满足通常的运算规则，则称集合 $\mathbb{V}$ 关于此加法和数乘是域 $\mathbb{F}$ 上的线性空间。（一般也把这种线性空间称为向量空间，$\mathbb{V}$ 中的元素称为向量）
注1：空间这个概念只是为了类比2维或3维几何空间的一个概念，更好的理解为元素的集合，线性空间中的元素统称为抽象向量
注2：集合 $\mathbb{V}$ 中的元素分别为数组、函数、有向线段时，对应的线性空间称为数域空间、函数空间、几何空间
注3：数域 $\mathbb{F}$ 上的标准线性空间 $\mathbb{F}^n$ （数域空间）
$\mathbb{V}:=\mathbb{F}^n=\begin{matrix}n\\ \overbrace{\mathbb{F}\times\mathbb{F}\times \cdots\times \mathbb{F} }\end{matrix}$ ，其元素称为 n元组（n-tuple）
加法：$\begin{bmatrix}v_1\\ \vdots\\ v_n\end{bmatrix} + \begin{bmatrix}w_1\\ \vdots\\ w_n\end{bmatrix} = \begin{bmatrix}v_1+w_1\\ \vdots\\ v_n+w_n\end{bmatrix}$
数乘：$\begin{bmatrix}v_1\\ \vdots\\ v_n\end{bmatrix}\cdot k=\begin{bmatrix}v_1\cdot k\\ \vdots\\ v_n\cdot k\end{bmatrix}$
容易证明，定义的加法和数乘满足上述运算规则
注4：对于几何空间（有向线段的集合），加法运算采用平行四边形或三角形法则进行计算，数乘运算表示对有向线段进行同向或反向伸缩
向量组：$\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_p$
抽象矩阵：$[\boldsymbol{\alpha}_1\ \boldsymbol{\alpha}_2\ \cdots\ \boldsymbol{\alpha}_p]$
定义方程组：
若无非零解，则向量组 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_p$ 线性无关；若存在非零解，则向量组 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_p$ 线性相关
定义方程组：
若有解，则向量 $\boldsymbol{\beta}$ 可由向量组 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_p$ 线性表出
定义方程组：
若有解，则向量组 $\boldsymbol{\beta}_1,\boldsymbol{\beta}_2,\cdots,\boldsymbol{\beta}_p$ 可由向量组 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_p$ 线性表出
向量组的线性表示具有传递性
设集合 $\mathbb{V}$ 是 数域 $\mathbb{F}$ 上的线性空间，有正整数 $n$ 及 $\mathbb{V}$ 中的向量组 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_n$ 满足以下两个条件：
线性无关性：向量组 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_n$ 线性无关
生成性：$\forall \boldsymbol{\alpha} \in \mathbb{V} $ ，均可由 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_n$ 线性表出
则称向量组 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_n$ 为 $n$ 维线性空间 $\mathbb{V}$ 的一组基，矩阵 $A=[\boldsymbol{\alpha}_1\ \boldsymbol{\alpha}_2\ \cdots\ \boldsymbol{\alpha}_n]$ 称为基矩阵，向量 $\boldsymbol{x}=[x_1\ x_2\ \cdots\ x_n]^T\in\mathbb{F}^n$ 称为抽象向量 $\boldsymbol{\alpha}$ 在基 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_n$ 下的坐标。
换言之，抽象向量 = 基矩阵 $\cdot$ 坐标向量
注1：基向量组的线性无关性保证线性空间中的抽象向量在该基下的坐标是唯一的，生成性保证空间中的任意向量在该基下都有坐标；
注2：基（坐标系）实现了抽象线性空间到标准线性空间的一一对应（通过基实现对抽象向量的具体化）
标准基：
标准基构成的基矩阵是单位矩阵 $\boldsymbol{I}_n=[\boldsymbol{e}_1\ \cdots\ \boldsymbol{e}_n]\in\mathbb{F}^{n\times n}$
一般基：向量组 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_n$ 是一般基 $\Leftrightarrow$ 线性无关 $\Leftrightarrow r(\boldsymbol{A})=n$ ，由一般基构成的基矩阵是非奇异矩阵
设 $\mathbb{V}$ 是 $\mathbb{F}$ 上的线性空间，$\mathbb{W}\subseteq \mathbb{V}$ 是非空子集，若 $\mathbb{W}$ 中的元素也满足加法封闭性和数乘封闭性，则称 $\mathbb{W}$ 是 $\mathbb{V}$ 的一个线性子空间。
设 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_p$ 是线性空间 $\mathbb{V}$ 中的一个向量组，定义集合 $\mathbb{W}$ 如下：
称 $\mathbb{W}$ 为向量组 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_p$ 的生成子空间，显然 $\mathbb{W}$ 是 $\mathbb{V}$ 的子空间。
设矩阵 $\boldsymbol{A}\in \mathbb{F}^{m\times n}$ ，定义矩阵 $\boldsymbol{A}$ 的核（kernel）与像（Image）如下：
显然，矩阵 $\boldsymbol{A}$ 的核即为齐次线性方程组的解空间 ，像即为由列向量组张成的子空间
设 $\mathbb{U}$ 和 $\mathbb{W}$ 是 $\mathbb{V}$ 的子空间，则
若 $f:A\rightarrow B$ 是一个映射，则须满足以下两个充要条件：
设 $\mathbb{V_1},\mathbb{V_2}$ 是域 $\mathbb{F}$ 上的线性空间，$\sigma:\mathbb{V_1}\rightarrow\mathbb{V_2}$ 是映射，若满足以下两个条件：
则称 $\sigma$ 是 $\mathbb{V_1}$ 到 $\mathbb{V_2}$ 的线性映射
若 $\mathbb{V_1}=\mathbb{V_2}=\mathbb{V}$ ，则称 $\sigma$ 为 $\mathbb{V}$ 上的线性变换
线性映射不同空间，线性变换同一空间
若 $\sigma$ 是可逆映射，则称其为线性同构（数学结构相同）。最典型的例子：抽象的线性空间选定基后，与标准线性空间线性同构
矩阵决定线性映射：给定 $\boldsymbol{A}\in\mathbb{F}^{m\times n}$ ，通过右乘列向量可以决定线性映射 $\sigma$ ：
线性映射决定矩阵：给定线性映射 $\sigma:\mathbb{V_1}\rightarrow\mathbb{V_2}$ ，一定能用某个矩阵 $\boldsymbol{A}$ 表示出来：
设 $\text{dim}(\mathbb{V_1})=n$ ，向量组 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_n$ 是空间 $\mathbb{V_1}$ 的一组基；$\text{dim}(\mathbb{V_2})=m$ ，向量组 $\boldsymbol{\beta}_1,\boldsymbol{\beta}_2,\cdots,\boldsymbol{\beta}_m$ 是空间 $\mathbb{V_2}$ 的一组基，则对 $\forall \boldsymbol{x}\in\mathbb{V_1}$ ，根据线性映射的保加性和保乘性，有：
称矩阵 $\boldsymbol{A}$ 为线性映射 $\sigma$ 在入口基 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_n$ 与出口基 $\boldsymbol{\beta}_1,\boldsymbol{\beta}_2,\cdots,\boldsymbol{\beta}_m$ 下的矩阵表示，写作：
线性映射 $\sigma$ 也可以用某个矩阵表示，即：
第 $i$ 列表示基向量 $\boldsymbol{\alpha}_i$ 在基 $\boldsymbol{\beta}_1,\boldsymbol{\beta}_2,\cdots,\boldsymbol{\beta}_m$ 下的坐标；像 $\sigma(\boldsymbol{x})$ 在基 $\boldsymbol{\beta}_1,\boldsymbol{\beta}_2,\cdots,\boldsymbol{\beta}_m$ 下的坐标为：
从线性变换看旋转矩阵
设矩阵 $\boldsymbol{A} ,\boldsymbol{B}\in\mathbb{F}^{m\times n}$ ，若存在可逆矩阵 $\boldsymbol{P}\in\mathbb{F}^{n\times n},\boldsymbol{Q}\in\mathbb{F}^{m\times m}$ ，使得 $\boldsymbol{AP}=\boldsymbol{QB}$ ，则称矩阵 $\boldsymbol{A},\boldsymbol{B}$ 等价；进一步，若 $m=n$ ，且 $\boldsymbol{AP}=\boldsymbol{PB}$ ，则称$\boldsymbol{A},\boldsymbol{B}$ 相似。
从几何角度理解矩阵等价与几何相似（进一步理解公式11）
将 $\boldsymbol{A}$ 视为标准线性空间 $\mathbb{F}^n$ 到 $\mathbb{F}^m$ 的线性映射：$\ \boldsymbol{x}\mapsto\boldsymbol{y}=\boldsymbol{Ax}$ （具体矩阵抽象化）或视为某组未知入口基和出口基下的矩阵表示（不妨都取为标准基 $\boldsymbol{E_n},\boldsymbol{E_m}$ ）
由 $\boldsymbol{P},\boldsymbol{Q}$ 可逆 $\Rightarrow$ 其列向量可视为 $\mathbb{F}^n$ / $\mathbb{F}^m$ 空间中的两个一般基矩阵。称 $\boldsymbol{P}=[p_1\ p_2\ \cdots\ p_n]$ 为入口基，$\boldsymbol{Q}=[q_1\ q_2\ \cdots q_m]$ 为出口基。
由于 $\boldsymbol{AP}=\boldsymbol{QB}$ ，所以有下图成立，等式左右均表示从一般基P下的坐标到标准基下的坐标的线性映射。
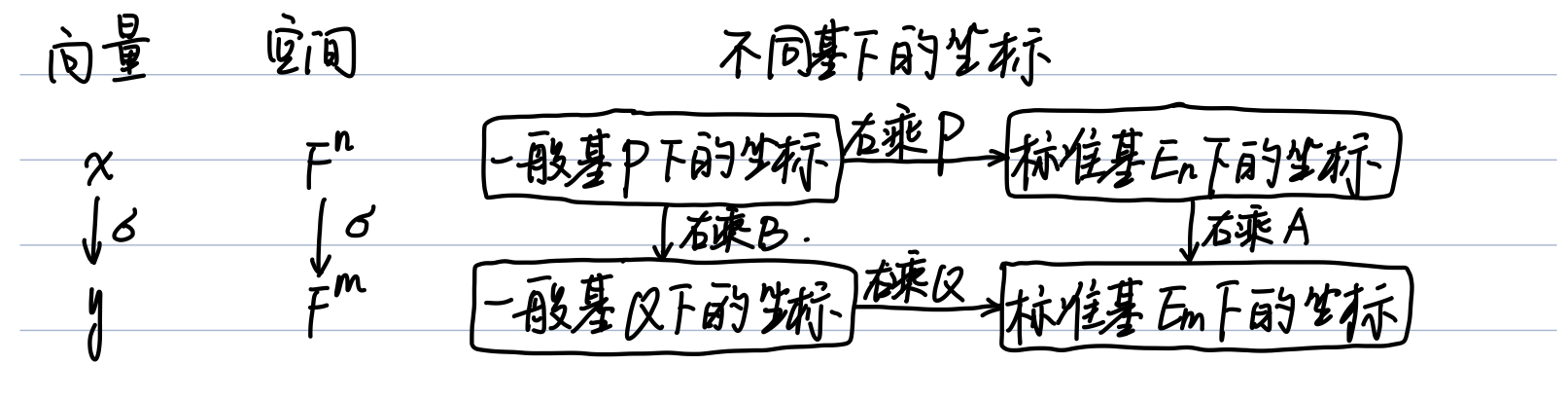
因此，矩阵等价的几何意义为：线性映射 $\boldsymbol{A}$ 在入口基 $\boldsymbol{P}$ 和出口基 $\boldsymbol{Q}$ 下的矩阵表示为 $\boldsymbol{B}$ ，换言之，相当于同一线性映射在不同基下的矩阵表示。
进一步，当 $m=n$ ，即在线性映射的两个空间是同一个空间的情况下，矩阵相似的几何意义为：同一线性变换在不同基下的矩阵表示。
设方阵 $\boldsymbol{A}\in\mathbb{F}^{n\times n}$ ，子空间 $\mathbb{W}\subseteq\mathbb{F}^n$ ，若满足 $\boldsymbol{A}(\mathbb{W})=\{\boldsymbol{Ax}|\boldsymbol{x}\in\mathbb{W}\}\subseteq\mathbb{W}$ ，即线性变换 $\boldsymbol{A}$ 作用在子空间 $\mathbb{W}$ 上的元素的像依然在子空间 $\mathbb{W}$ 中，则称 $\mathbb{W}$ 是 $\boldsymbol{A}$ 的不变子空间。典型的不变子空间包括：$\{0\},\mathbb{F}^n,\text{ker}(\boldsymbol{A}),\text{im}(\boldsymbol{A})$
不变子空间等同于相似三角化
对相似方阵 $\boldsymbol{A},\boldsymbol{B}\in\mathbb{F}^{n\times n}$ ，有可逆矩阵 $\boldsymbol{P}$ 使得 $\boldsymbol{AP}=\boldsymbol{PB}$ ，将矩阵 $\boldsymbol{P}$ 写作分块矩阵 $\boldsymbol{P}=[\boldsymbol{P_{1,n\times n_1}}|\boldsymbol{P_{2,n\times (n-n_1)}} ]$ ，对应地，将矩阵 $\boldsymbol{B}$ 写作分块矩阵：
则：
下面给出证明：
即：
若 $\boldsymbol{B_{21}}=\boldsymbol{0}$ ，则 $\boldsymbol{AP_1}=\boldsymbol{P_1B_{11}}$ ，即 $\boldsymbol{A}\cdot\boldsymbol{p_{1j}}$ 均可由 $\boldsymbol{P_1}$ 的列向量的线性组合表出，而 $\boldsymbol{P_1}$ 的列向量的所有线性组合即为 $\text{im}\boldsymbol{P_1}\subseteq\mathbb{F}^{n_1}\subseteq\mathbb{F}^n$ ，从而 $\boldsymbol{A}$ 作用在子空间 $\text{im}\boldsymbol{P_1}$ 上的元素的像依然在子空间 $\text{im}\boldsymbol{P_1}$ 中，因此结论成立。
从不变子空间到相似三角化
给定方阵 $\boldsymbol{A}$ 和子空间 $\mathbb{W}$ ，求矩阵 $\boldsymbol{P}$ 使得相似矩阵 $\boldsymbol{B}$ 块三角化。
$\Leftrightarrow$ 将 $\mathbb{W}$ 的 $n_1$ 个基向量扩充为 $\mathbb{F}^n$ 的一组基（因为 $\boldsymbol{P}$ 可逆），由这组基组成所求矩阵 $\boldsymbol{P}$
从相似三角化到不变子空间
给定矩阵 $\boldsymbol{P}$ ，求不变子空间 $\mathbb{W}$ 。
根据不变子空间的维数 $n_1$ ，取 $\boldsymbol{P}$ 的前 $n_1$ 列向量张成即可。
特征向量满足： $\boldsymbol{A}\boldsymbol{p}=\boldsymbol{p}\lambda,\boldsymbol{A}\in\mathbb{F}^{n\times n},\boldsymbol{p}\in\mathbb{F}^n,\lambda\in\mathbb{F}$ ，显然等式右侧向量也在子空间 $\text{im}\boldsymbol{p}$ 中，所以 $\text{im}\boldsymbol{p}$ 为 $\boldsymbol{A}$ 的一维不变子空间。
即，矩阵的一维不变子空间对应的向量即为特征向量，特征向量对应的特征值可以不只一个。
由上可知，$\boldsymbol{P}=[\boldsymbol{p}_1\ \cdots \ \boldsymbol{p}_n]$ ，因此：
可以相似对角化 $\Leftrightarrow\forall j,\ \text{im}\boldsymbol{p}_j$ 是 $\boldsymbol{A}$ 的不变子空间 $\Leftrightarrow\forall j,\boldsymbol{p}_j$ 是 $\boldsymbol{A}$ 的特征向量 $\Leftrightarrow$ 矩阵 $\boldsymbol{A}$ 有 $n$ 个线性无关的特征向量 $\Leftrightarrow$ 矩阵 $\boldsymbol{A}$ 有一组由特征向量构成的基
从几何角度理解相似对角化，上述结论也是显然的：
并不是所有矩阵都有 $n$ 个特征向量，即并不是所有矩阵都能相似对角化，对于不能相似对角化的矩阵，我们提出 Jordan(若当)标准型 的概念。