矩阵分析学习笔记1：线性空间与线性映射

Chapter1 线性空间与线性映射

线性空间

域 $\mathbb{F}$

一个域是一个运算系统，包括一个集合和在集合上定义的两种运算（加法和乘法）且两种运算都满足一定的运算规则

常用域：有理数域 $\mathbb{Q}$ ，实数域 $\mathbb{R}$ ，复数域 $\mathbb{C}$

二元加法运算+

给定非空集合 $\mathbb{V}$ 和域 $\mathbb{F}$ ，若存在映射 $\sigma:\mathbb{V}\times \mathbb{V}\rightarrow \mathbb{V},(\boldsymbol{\alpha},\boldsymbol{\beta})\mapsto\sigma(\boldsymbol{\alpha},\boldsymbol{\beta})$ ，即对集合 $\mathbb{V}$ 中的任意元素 $\boldsymbol{\alpha},\boldsymbol{\beta}$ ，在集合 $\mathbb{V}$ 中都存在唯一元素 $\boldsymbol{\gamma}$ ，使得 $\boldsymbol{\gamma}=\boldsymbol{\alpha}+\boldsymbol{\beta}\in\mathbb{V}$，则称 $\sigma$ 为集合 $\mathbb{V}$ 上的加法 。

注：定义中的 $\times$ 是集合之间的乘法，称为卡氏积/笛卡尔积，指的是从两个集合中任取一个元素组成的所有有序元素对的集合：$\mathbb{S_1}\times\mathbb{S_2}=\{(a,b)|a\in\mathbb{S_1},b\in\mathbb{S_2}\}$

二元数乘运算 $\cdot$

给定非空集合 $\mathbb{V}$ 和数域 $\mathbb{F}$ ，若存在映射 $\sigma:\mathbb{V}\times \mathbb{F}\rightarrow \mathbb{V},(\boldsymbol{\alpha},k)\mapsto\sigma(\boldsymbol{\alpha},k)$ ，即对集合 $\mathbb{V}$ 中的任意元素 $\boldsymbol{\alpha}$ 和数域 $\mathbb{F}$ 中的任意元素 $k$ ，在集合 $\mathbb{V}$ 中都存在唯一元素 $\boldsymbol{\gamma}$ ，使得 $\boldsymbol{\gamma}=\boldsymbol{\alpha}\cdot k\in\mathbb{V}$，则称 $\sigma$ 为集合 $\mathbb{V}$ 上的数乘 。

通常的运算规则

1. 加法的运算规则
   • 交换律：$\boldsymbol{\alpha}+\boldsymbol{\beta}=\boldsymbol{\beta}+\boldsymbol{\alpha}$
   • 结合律：$(\boldsymbol{\alpha}+\boldsymbol{\beta})+\boldsymbol{\gamma}=\boldsymbol{\alpha}+(\boldsymbol{\beta}+\boldsymbol{\gamma})$
   • 有零元：$\exists \boldsymbol{e}\in\mathbb{V},s.t.\ \boldsymbol{e}+\boldsymbol{\alpha}=\boldsymbol{\alpha}\ 对\ \forall \boldsymbol{\alpha}\in\mathbb{V}\ 成立$
   • 有逆元：$对\ \forall\boldsymbol{\alpha}\in\mathbb{V},\exists\boldsymbol{\beta}\in\mathbb{V},s.t.\ \boldsymbol{\alpha}+\boldsymbol{\beta}=\boldsymbol{e},记\ \boldsymbol{\beta}=-\boldsymbol{\alpha}$
2. 数乘的运算规则
   • 交换律：$\boldsymbol{\alpha}\cdot k=k\cdot\boldsymbol{\alpha}$ （一般将对列向量数乘的数写在右侧，对行向量数乘的数写在左侧，这样可以和矩阵乘法作类比）
   • 结合律：$(\boldsymbol{\alpha}\cdot k)\cdot l=\boldsymbol{\alpha}\cdot (kl)$ （注：左边做了两次数乘，右边做了一次 $\mathbb{F}$ 中数的乘法和一次数乘）
   • 分配律：$(\boldsymbol{\alpha}+\boldsymbol{\beta})\cdot k=\boldsymbol{\alpha}\cdot k+\boldsymbol{\beta}\cdot k,\quad \boldsymbol{\alpha}\cdot(k_1+k_2)=\boldsymbol{\alpha}\cdot k_1 + \boldsymbol{\alpha}\cdot k_2$ （注：第二个式子左边做的是 $\mathbb{F}$ 中数的加法，右边做的是向量加法）
   • 与 $\mathbb{F}$ 中 1 的关系：$\boldsymbol{\alpha}\cdot 1=\boldsymbol{\alpha}$

线性空间

若集合 $\mathbb{V}$ 满足上述两种运算，且这两种运算满足通常的运算规则，则称集合 $\mathbb{V}$ 关于此加法和数乘是域 $\mathbb{F}$ 上的线性空间。（一般也把这种线性空间称为向量空间，$\mathbb{V}$ 中的元素称为向量）

注1：空间这个概念只是为了类比2维或3维几何空间的一个概念，更好的理解为元素的集合，线性空间中的元素统称为抽象向量

注2：集合 $\mathbb{V}$ 中的元素分别为数组、函数、有向线段时，对应的线性空间称为数域空间、函数空间、几何空间

注3：数域 $\mathbb{F}$ 上的标准线性空间 $\mathbb{F}^n$ （数域空间）

​ $\mathbb{V}:=\mathbb{F}^n=\begin{matrix}n\\ \overbrace{\mathbb{F}\times\mathbb{F}\times \cdots\times \mathbb{F} }\end{matrix}$ ，其元素称为 n元组（n-tuple）

​ 加法：$\begin{bmatrix}v_1\\ \vdots\\ v_n\end{bmatrix} + \begin{bmatrix}w_1\\ \vdots\\ w_n\end{bmatrix} = \begin{bmatrix}v_1+w_1\\ \vdots\\ v_n+w_n\end{bmatrix}$

​ 数乘：$\begin{bmatrix}v_1\\ \vdots\\ v_n\end{bmatrix}\cdot k=\begin{bmatrix}v_1\cdot k\\ \vdots\\ v_n\cdot k\end{bmatrix}$

​ 容易证明，定义的加法和数乘满足上述运算规则

注4：对于几何空间（有向线段的集合），加法运算采用平行四边形或三角形法则进行计算，数乘运算表示对有向线段进行同向或反向伸缩

向量组的线性相关性

向量组：$\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_p$

抽象矩阵：$[\boldsymbol{\alpha}_1\ \boldsymbol{\alpha}_2\ \cdots\ \boldsymbol{\alpha}_p]$

定义方程组：

$$\boldsymbol{A}\boldsymbol{x}=[\boldsymbol{\alpha}_1\ \boldsymbol{\alpha}_2\ \cdots\ \boldsymbol{\alpha}_p]\begin{bmatrix}x_1\\x_2\\ \vdots\\ x_p \end{bmatrix}=\boldsymbol{0}$$

若无非零解，则向量组 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_p$ 线性无关；若存在非零解，则向量组 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_p$ 线性相关

向量组的线性表出

定义方程组：

$$\boldsymbol{A}\boldsymbol{x}=[\boldsymbol{\alpha}_1\ \boldsymbol{\alpha}_2\ \cdots\ \boldsymbol{\alpha}_p]\begin{bmatrix}x_1\\x_2\\ \vdots\\ x_p \end{bmatrix}=\boldsymbol{\beta}$$

若有解，则向量 $\boldsymbol{\beta}$ 可由向量组 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_p$ 线性表出

定义方程组：

$$\boldsymbol{A}\boldsymbol{X}=[\boldsymbol{\alpha}_1\ \boldsymbol{\alpha}_2\ \cdots\ \boldsymbol{\alpha}_p] \begin{bmatrix} x_{11} &x_{12}\ \ \cdots&x_{1p} \\ x_{21} &x_{22}\ \ \cdots&x_{2p} \\ \vdots &\ddots &\vdots \\ x_{p1} &x_{p2}\ \ \cdots&x_{pp} \end{bmatrix} =[\boldsymbol{\beta}_1\ \boldsymbol{\beta}_2\ \cdots\ \boldsymbol{\beta}_p] =\boldsymbol{B}$$

若有解，则向量组 $\boldsymbol{\beta}_1,\boldsymbol{\beta}_2,\cdots,\boldsymbol{\beta}_p$ 可由向量组 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_p$ 线性表出

向量组的线性表示具有传递性

有限维线性空间的基（坐标系）与坐标

设集合 $\mathbb{V}$ 是 数域 $\mathbb{F}$ 上的线性空间，有正整数 $n$ 及 $\mathbb{V}$ 中的向量组 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_n$ 满足以下两个条件：

• 线性无关性：向量组 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_n$ 线性无关

• 生成性：$\forall \boldsymbol{\alpha} \in \mathbb{V} $ ，均可由 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_n$ 线性表出

  $$\boldsymbol{\alpha}=[\boldsymbol{\alpha}_1\ \boldsymbol{\alpha}_2\ \cdots\ \boldsymbol{\alpha}_n]\begin{bmatrix}x_1\\x_2\\ \vdots\\ x_n \end{bmatrix}=\boldsymbol{A}\boldsymbol{x}$$

则称向量组 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_n$ 为 $n$ 维线性空间 $\mathbb{V}$ 的一组基，矩阵 $A=[\boldsymbol{\alpha}_1\ \boldsymbol{\alpha}_2\ \cdots\ \boldsymbol{\alpha}_n]$ 称为基矩阵，向量 $\boldsymbol{x}=[x_1\ x_2\ \cdots\ x_n]^T\in\mathbb{F}^n$ 称为抽象向量 $\boldsymbol{\alpha}$ 在基 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_n$ 下的坐标。

换言之，抽象向量 = 基矩阵 $\cdot$ 坐标向量

注1：基向量组的线性无关性保证线性空间中的抽象向量在该基下的坐标是唯一的，生成性保证空间中的任意向量在该基下都有坐标；

注2：基（坐标系）实现了抽象线性空间到标准线性空间的一一对应（通过基实现对抽象向量的具体化）

标准线性空间 $\mathbb{F}^n$ 的标准基与一般基

标准基：

$$\boldsymbol{e}_1=\begin{bmatrix}1\\0\\\vdots\\0 \end{bmatrix}, \boldsymbol{e}_2=\begin{bmatrix}0\\1\\\vdots\\0 \end{bmatrix} \boldsymbol{e}_n=\begin{bmatrix}0\\0\\\vdots\\1 \end{bmatrix}, \text{and}\ \boldsymbol{e}_i\in\mathbb{F}^n$$

标准基构成的基矩阵是单位矩阵 $\boldsymbol{I}_n=[\boldsymbol{e}_1\ \cdots\ \boldsymbol{e}_n]\in\mathbb{F}^{n\times n}$

一般基：向量组 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_n$ 是一般基 $\Leftrightarrow$ 线性无关 $\Leftrightarrow r(\boldsymbol{A})=n$ ，由一般基构成的基矩阵是非奇异矩阵

线性子空间

设 $\mathbb{V}$ 是 $\mathbb{F}$ 上的线性空间，$\mathbb{W}\subseteq \mathbb{V}$ 是非空子集，若 $\mathbb{W}$ 中的元素也满足加法封闭性和数乘封闭性，则称 $\mathbb{W}$ 是 $\mathbb{V}$ 的一个线性子空间。

向量组的生成子空间和子空间的生成组

设 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_p$ 是线性空间 $\mathbb{V}$ 中的一个向量组，定义集合 $\mathbb{W}$ 如下：

$$\mathbb{W}=\text{span} \{ \boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_p \} =\{ \boldsymbol{\alpha}_1\cdot x_1+\boldsymbol{\alpha}_2\cdot x_2+\cdots+\boldsymbol{\alpha}_p\cdot x_p|\forall x_i\in\mathbb{F} \}$$

称 $\mathbb{W}$ 为向量组 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_p$ 的生成子空间，显然 $\mathbb{W}$ 是 $\mathbb{V}$ 的子空间。

矩阵的核与像

设矩阵 $\boldsymbol{A}\in \mathbb{F}^{m\times n}$ ，定义矩阵 $\boldsymbol{A}$ 的核（kernel）与像（Image）如下：

$$\text{ker}\boldsymbol{A}=\{\boldsymbol{x}|\boldsymbol{A}\boldsymbol{x}=\boldsymbol{0},\boldsymbol{x}\in \mathbb{F}^n\} \subseteq \mathbb{F}^n \\ \text{Im}\boldsymbol{A}=\{\boldsymbol{A}\boldsymbol{x}|\forall \boldsymbol{x}\in \mathbb{F}^n\} \subseteq \mathbb{F}^m$$

显然，矩阵 $\boldsymbol{A}$ 的核即为齐次线性方程组的解空间 ，像即为由列向量组张成的子空间

子空间的交与和

设 $\mathbb{U}$ 和 $\mathbb{W}$ 是 $\mathbb{V}$ 的子空间，则

• $\mathbb{U}\cap\mathbb{W}$ 也是子空间，称为 $\mathbb{U}$ 和 $\mathbb{W}$ 的交（子空间）
• $\mathbb{U}+\mathbb{W}=\text{span}\{\mathbb{U},\mathbb{W}\}=\{u+w|\forall u\in\mathbb{U},w\in\mathbb{W}\}$ 也是子空间，称为 $\mathbb{U}$ 和 $\mathbb{W}$ 的和（子空间）
• 但 $\mathbb{U}\cup\mathbb{W}$ 不一定是子空间！

线性映射

映射

若 $f:A\rightarrow B$ 是一个映射，则须满足以下两个充要条件：

• 存在性：$\forall a\in A,\exists b\in B$ 与之对应
• 唯一性：$\forall a\in A$，在 $B$ 中的像 $b$ 是唯一的

线性映射，线性变换与线性同构

设 $\mathbb{V_1},\mathbb{V_2}$ 是域 $\mathbb{F}$ 上的线性空间，$\sigma:\mathbb{V_1}\rightarrow\mathbb{V_2}$ 是映射，若满足以下两个条件：

• 保加性：$\forall v_1,v_2\in\mathbb{V_1},\sigma(v_1+v_2)=\sigma(v_1)+\sigma(v_2)\in\mathbb{V_2}$
• 保乘性：$\forall v\in\mathbb{V_1},\sigma(v\cdot k)=\sigma(v)\cdot k\in\mathbb{V_2}$

则称 $\sigma$ 是 $\mathbb{V_1}$ 到 $\mathbb{V_2}$ 的线性映射

若 $\mathbb{V_1}=\mathbb{V_2}=\mathbb{V}$ ，则称 $\sigma$ 为 $\mathbb{V}$ 上的线性变换

线性映射不同空间，线性变换同一空间

若 $\sigma$ 是可逆映射，则称其为线性同构（数学结构相同）。最典型的例子：抽象的线性空间选定基后，与标准线性空间线性同构

矩阵 与 标准线性空间中的线性映射 是等同的

1. 矩阵决定线性映射：给定 $\boldsymbol{A}\in\mathbb{F}^{m\times n}$ ，通过右乘列向量可以决定线性映射 $\sigma$ ：

   $$\sigma:\mathbb{V_1}\rightarrow\mathbb{V_2};\ \boldsymbol{x}\mapsto\boldsymbol{y}=\boldsymbol{Ax}$$

2. 线性映射决定矩阵：给定线性映射 $\sigma:\mathbb{V_1}\rightarrow\mathbb{V_2}$ ，一定能用某个矩阵 $\boldsymbol{A}$ 表示出来：

   设 $\text{dim}(\mathbb{V_1})=n$ ，向量组 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_n$ 是空间 $\mathbb{V_1}$ 的一组基；$\text{dim}(\mathbb{V_2})=m$ ，向量组 $\boldsymbol{\beta}_1,\boldsymbol{\beta}_2,\cdots,\boldsymbol{\beta}_m$ 是空间 $\mathbb{V_2}$ 的一组基，则对 $\forall \boldsymbol{x}\in\mathbb{V_1}$ ，根据线性映射的保加性和保乘性，有：

   $$\begin{align} \sigma(\boldsymbol{x})&=\sigma([\boldsymbol{\alpha}_1\ \boldsymbol{\alpha}_2\ \cdots\ \boldsymbol{\alpha}_n]\boldsymbol{x}) \notag\\ &=\sigma(\boldsymbol{\alpha}_1x_1+\boldsymbol{\alpha}_2x_2+\cdots+\boldsymbol{\alpha}_nx_n) \notag\\ &=\sigma(\boldsymbol{\alpha}_1x_1)+\sigma(\boldsymbol{\alpha}_2x_2)+\cdots+\sigma(\boldsymbol{\alpha}_nx_n) \notag \\ &=\sigma(\boldsymbol{\alpha}_1)x_1+\sigma(\boldsymbol{\alpha}_2)x_2+\cdots+\sigma(\boldsymbol{\alpha}_n)x_n \\ &=[\sigma(\boldsymbol{\alpha}_1)\ \sigma(\boldsymbol{\alpha}_2)\ \cdots\ \sigma(\boldsymbol{\alpha}_n) ]\begin{bmatrix}x_1\\x_2\\ \vdots \\x_n \end{bmatrix} \notag \\ &=[\boldsymbol{\beta}_1\ \boldsymbol{\beta}_2\ \cdots\ \boldsymbol{\beta}_m]\boldsymbol{Ax} \notag \end{align}$$

   称矩阵 $\boldsymbol{A}$ 为线性映射 $\sigma$ 在入口基 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_n$ 与出口基 $\boldsymbol{\beta}_1,\boldsymbol{\beta}_2,\cdots,\boldsymbol{\beta}_m$ 下的矩阵表示，写作：

   $$\sigma[\boldsymbol{\alpha}_1\ \boldsymbol{\alpha}_2\ \cdots\ \boldsymbol{\alpha}_n] =[\boldsymbol{\beta}_1\ \boldsymbol{\beta}_2\ \cdots\ \boldsymbol{\beta}_m]\boldsymbol{A}$$

   线性映射 $\sigma$ 也可以用某个矩阵表示，即：

   $$\begin{bmatrix}线性\\映射\end{bmatrix} \begin{bmatrix}入\\口\\基\end{bmatrix}= \begin{bmatrix}出\\口\\基\end{bmatrix} \begin{bmatrix}矩阵\\表示\end{bmatrix}$$

   第 $i$ 列表示基向量 $\boldsymbol{\alpha}_i$ 在基 $\boldsymbol{\beta}_1,\boldsymbol{\beta}_2,\cdots,\boldsymbol{\beta}_m$ 下的坐标；像 $\sigma(\boldsymbol{x})$ 在基 $\boldsymbol{\beta}_1,\boldsymbol{\beta}_2,\cdots,\boldsymbol{\beta}_m$ 下的坐标为：

   $$\boldsymbol{y}=\begin{bmatrix}y_1\\y_2\\ \vdots \\y_m \end{bmatrix}=\boldsymbol{A}\begin{bmatrix}x_1\\x_2\\ \vdots \\ \vdots \\x_n \end{bmatrix}=\boldsymbol{Ax}$$

• 从线性变换看旋转矩阵

  

矩阵等价与矩阵相似（重点：用线性空间和线性映射的观点重新认知）

设矩阵 $\boldsymbol{A} ,\boldsymbol{B}\in\mathbb{F}^{m\times n}$ ，若存在可逆矩阵 $\boldsymbol{P}\in\mathbb{F}^{n\times n},\boldsymbol{Q}\in\mathbb{F}^{m\times m}$ ，使得 $\boldsymbol{AP}=\boldsymbol{QB}$ ，则称矩阵 $\boldsymbol{A},\boldsymbol{B}$ 等价；进一步，若 $m=n$ ，且 $\boldsymbol{AP}=\boldsymbol{PB}$ ，则称$\boldsymbol{A},\boldsymbol{B}$ 相似。

从几何角度理解矩阵等价与几何相似（进一步理解公式11）

​ 将 $\boldsymbol{A}$ 视为标准线性空间 $\mathbb{F}^n$ 到 $\mathbb{F}^m$ 的线性映射：$\ \boldsymbol{x}\mapsto\boldsymbol{y}=\boldsymbol{Ax}$ （具体矩阵抽象化）或视为某组未知入口基和出口基下的矩阵表示（不妨都取为标准基 $\boldsymbol{E_n},\boldsymbol{E_m}$ ）

​ 由 $\boldsymbol{P},\boldsymbol{Q}$ 可逆 $\Rightarrow$ 其列向量可视为 $\mathbb{F}^n$ / $\mathbb{F}^m$ 空间中的两个一般基矩阵。称 $\boldsymbol{P}=[p_1\ p_2\ \cdots\ p_n]$ 为入口基，$\boldsymbol{Q}=[q_1\ q_2\ \cdots q_m]$ 为出口基。

​ 由于 $\boldsymbol{AP}=\boldsymbol{QB}$ ，所以有下图成立，等式左右均表示从一般基P下的坐标到标准基下的坐标的线性映射。

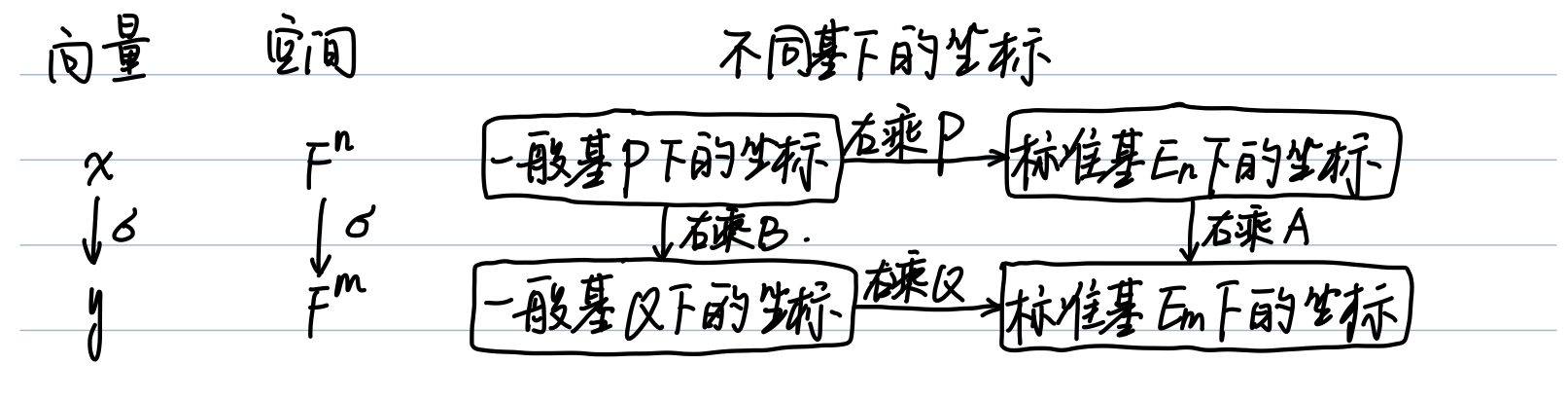
​ 因此，矩阵等价的几何意义为：线性映射 $\boldsymbol{A}$ 在入口基 $\boldsymbol{P}$ 和出口基 $\boldsymbol{Q}$ 下的矩阵表示为 $\boldsymbol{B}$ ，换言之，相当于同一线性映射在不同基下的矩阵表示。

​ 进一步，当 $m=n$ ，即在线性映射的两个空间是同一个空间的情况下，矩阵相似的几何意义为：同一线性变换在不同基下的矩阵表示。

方阵(线性变换)的不变子空间

设方阵 $\boldsymbol{A}\in\mathbb{F}^{n\times n}$ ，子空间 $\mathbb{W}\subseteq\mathbb{F}^n$ ，若满足 $\boldsymbol{A}(\mathbb{W})=\{\boldsymbol{Ax}|\boldsymbol{x}\in\mathbb{W}\}\subseteq\mathbb{W}$ ，即线性变换 $\boldsymbol{A}$ 作用在子空间 $\mathbb{W}$ 上的元素的像依然在子空间 $\mathbb{W}$ 中，则称 $\mathbb{W}$ 是 $\boldsymbol{A}$ 的不变子空间。典型的不变子空间包括：$\{0\},\mathbb{F}^n,\text{ker}(\boldsymbol{A}),\text{im}(\boldsymbol{A})$

不变子空间等同于相似三角化

对相似方阵 $\boldsymbol{A},\boldsymbol{B}\in\mathbb{F}^{n\times n}$ ，有可逆矩阵 $\boldsymbol{P}$ 使得 $\boldsymbol{AP}=\boldsymbol{PB}$ ，将矩阵 $\boldsymbol{P}$ 写作分块矩阵 $\boldsymbol{P}=[\boldsymbol{P_{1,n\times n_1}}|\boldsymbol{P_{2,n\times (n-n_1)}} ]$ ，对应地，将矩阵 $\boldsymbol{B}$ 写作分块矩阵：

$$\boldsymbol{B}=\left[ \begin{array}{c|c} \boldsymbol{B}_{11,n_1\times n_1} & \boldsymbol{B}_{12,n_1\times(n-n_1)} \\ \hline \boldsymbol{B}_{21,(n-n_1)\times n_1} & \boldsymbol{B}_{22,(n-n_1)\times(n-n_1)} \end{array} \right]$$

则：

• $\boldsymbol{B}_{21}=\boldsymbol{0}\Leftrightarrow\text{im}\boldsymbol{P_1}$ 是 $\boldsymbol{A}$ 的不变子空间（上三角化）
• $\boldsymbol{B}_{12}=\boldsymbol{0}\Leftrightarrow\text{im}\boldsymbol{P_2}$ 是 $\boldsymbol{A}$ 的不变子空间（下三角化）

下面给出证明：

$$\boldsymbol{AP_1}=[\boldsymbol{P_1}|\boldsymbol{P_2}] \begin{bmatrix} \boldsymbol{B_{11}}\\ \boldsymbol{B_{21}} \end{bmatrix}$$

即：

$$\boldsymbol{AP_1}=\boldsymbol{P_1B_{11}}+\boldsymbol{P_2B_{21}}$$

若 $\boldsymbol{B_{21}}=\boldsymbol{0}$ ，则 $\boldsymbol{AP_1}=\boldsymbol{P_1B_{11}}$ ，即 $\boldsymbol{A}\cdot\boldsymbol{p_{1j}}$ 均可由 $\boldsymbol{P_1}$ 的列向量的线性组合表出，而 $\boldsymbol{P_1}$ 的列向量的所有线性组合即为 $\text{im}\boldsymbol{P_1}\subseteq\mathbb{F}^{n_1}\subseteq\mathbb{F}^n$ ，从而 $\boldsymbol{A}$ 作用在子空间 $\text{im}\boldsymbol{P_1}$ 上的元素的像依然在子空间 $\text{im}\boldsymbol{P_1}$ 中，因此结论成立。

从不变子空间到相似三角化

给定方阵 $\boldsymbol{A}$ 和子空间 $\mathbb{W}$ ，求矩阵 $\boldsymbol{P}$ 使得相似矩阵 $\boldsymbol{B}$ 块三角化。

$\Leftrightarrow$ 将 $\mathbb{W}$ 的 $n_1$ 个基向量扩充为 $\mathbb{F}^n$ 的一组基（因为 $\boldsymbol{P}$ 可逆），由这组基组成所求矩阵 $\boldsymbol{P}$

从相似三角化到不变子空间

给定矩阵 $\boldsymbol{P}$ ，求不变子空间 $\mathbb{W}$ 。

根据不变子空间的维数 $n_1$ ，取 $\boldsymbol{P}$ 的前 $n_1$ 列向量张成即可。

从一维不变子空间看特征向量

特征向量满足： $\boldsymbol{A}\boldsymbol{p}=\boldsymbol{p}\lambda,\boldsymbol{A}\in\mathbb{F}^{n\times n},\boldsymbol{p}\in\mathbb{F}^n,\lambda\in\mathbb{F}$ ，显然等式右侧向量也在子空间 $\text{im}\boldsymbol{p}$ 中，所以 $\text{im}\boldsymbol{p}$ 为 $\boldsymbol{A}$ 的一维不变子空间。

即，矩阵的一维不变子空间对应的向量即为特征向量，特征向量对应的特征值可以不只一个。

相似对角化的充要条件

由上可知，$\boldsymbol{P}=[\boldsymbol{p}_1\ \cdots \ \boldsymbol{p}_n]$ ，因此：

可以相似对角化 $\Leftrightarrow\forall j,\ \text{im}\boldsymbol{p}_j$ 是 $\boldsymbol{A}$ 的不变子空间 $\Leftrightarrow\forall j,\boldsymbol{p}_j$ 是 $\boldsymbol{A}$ 的特征向量 $\Leftrightarrow$ 矩阵 $\boldsymbol{A}$ 有 $n$ 个线性无关的特征向量 $\Leftrightarrow$ 矩阵 $\boldsymbol{A}$ 有一组由特征向量构成的基

从几何角度理解相似对角化，上述结论也是显然的：

$$\begin{align} \boldsymbol{P}^{-1}\boldsymbol{AP}=\boldsymbol{\Lambda}&\Leftrightarrow\boldsymbol{AP}=\boldsymbol{P\Lambda} \notag \\ &\Leftrightarrow\boldsymbol{A}[\boldsymbol{p}_1\cdots\boldsymbol{p}_n]=[\boldsymbol{p}_1\cdots\boldsymbol{p}_n] \begin{bmatrix} \lambda_1 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \lambda_n \end{bmatrix} \\ &\Leftrightarrow\forall j,\boldsymbol{A}\boldsymbol{p}_j=\boldsymbol{p}_j\lambda_j \notag \end{align}$$

从相似最简型问题到$\lambda$ 矩阵的Jordan标准型

并不是所有矩阵都有 $n$ 个特征向量，即并不是所有矩阵都能相似对角化，对于不能相似对角化的矩阵，我们提出 Jordan(若当)标准型 的概念。