Brief Introduction of Deep Learning

Brief Introduction of Deep Learning

3 steps of Deep Learning

• define a set of function
• goodness of function
• pick the best function

Neural Network

不同的连接方法（logistic regression）形成了不同的网络结构

网络参数 $\boldsymbol{\theta}$ 由所有 logistic regression 各自的weight $\boldsymbol{w}$ 和bias $b$ 组成

如何连接各个logistic regression？

全连接前馈网络 Fully Connect Feedforward Network

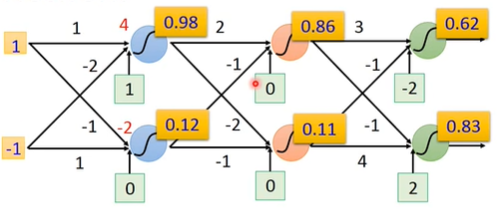
所以可以把一个neural network看成一个function，输入一个vector，输出一个vector：

$$f\Big(\Big[\begin{matrix}1 \\-1 \end{matrix}\Big]\Big)=\Big[\begin{matrix}0 .62\\0.83 \end{matrix}\Big]$$

一个 network structure 即为一个 function set

进一步扩大每一级的neuron个数，得到：

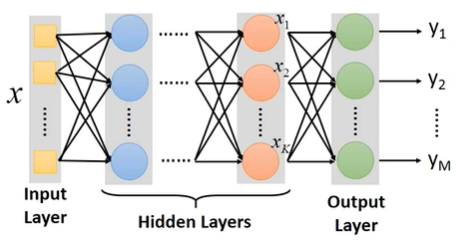
Hidden Layers：代替之前的feature engineering / feature transformation去完成特征提取的工作

Deep：即很多的Hidden Layers

• AlexNet（8层）VGG（19层）GoogleNet（22层）Residual Net（152层）

可以把输出层前一层的 $\boldsymbol{x}^k$ 看作一组变换后的特征向量，这个特征向量可以由一个简单的多分类器（Output Layer）完成分类

用矩阵运算表示网络运作流程

$$\sigma(\boldsymbol{w}^1\boldsymbol{x}+b^1)=\boldsymbol{a}^1\\ \sigma(\boldsymbol{w}^2\boldsymbol{a}^1+b^2)=\boldsymbol{a}^2\\ \cdots\\ \sigma(\boldsymbol{w}^{L}\boldsymbol{a}^{L-1}+b^L)=\boldsymbol{y}$$

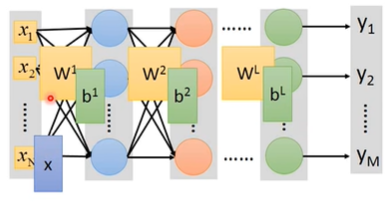
其中的 $\sigma$ 函数就是激活函数

因为把输出层用作一个多分类器，所以最后一层的激活函数应该使用Softmax

写成矩阵运算的好处=>可以用GPU加速

以手写数字识别为例

对一个16 $\times$ 16分辨率的图片来说，网络的输入即为一个256维的向量，输出则为一个10维的向量，每一维代表了这张图片等于0/1/…/9的概率

中间的整个网络结构就相当于定义了一个手写数字识别的 function set，要做的就是用Gradient Descent 去确定这个function的所有参数。在此过程中，需要决定用什么layer，多少layer，每个layer多少neuron，这就决定了function set是否有效。

怎么决定？ 经验和直觉

原来 => 怎么抽取特征。Feature Engineering / Feature Transform，找到一组好的feature

现在 => 怎么设计网络结构。

如何定义一组参数的好坏：依旧Cross Entropy

分类问题用交叉熵

$$C^i=\text{CrossEntropy}(\boldsymbol{y^i},\hat{\boldsymbol{y}}^i)\\ \text{Total_Loss}=\sum_{i=1}^nC^i$$

找到一组参数 $\boldsymbol{\theta}=[w_1,w_2…,b_1,b_2,…]$ 使 Total_Loss 最小（这里把向量 $\boldsymbol{w}$ 都拆开了）

Gradient Descent

1. 给 $\boldsymbol{\theta}$ 随机赋初始值
2. 计算梯度，例如$\frac{\partial L}{\partial {w_1}}$
3. 更新参数，例如$w_1\leftarrow w_1-\mu\frac{\partial L}{\partial {w_1}}$
4. 重复2、3两步，直到梯度小于某一阈值

Backpropagation

一个网络的参数可达百万甚至更多，Backpropagation 是一个比较有效率的计算参数微分（即梯度）的方式

为什么网络越深越好？

• Deep —> Modularization（模组化）类似函数调用

  把一个问题分成几个小问题，分步骤解决。每层网络都能自动从上一层学到更复杂的特征

  在数据量不大的情况下依然能学到较好的表现

  因为没有足够多的数据，所以要deep learning让机器去学习，不然直接查找就好了