Logistic Regression（以二分类为例）

Logistic Regression（以二分类为例）

2021/03/23

Step 1：Function Set

上节得到：

$$P(C_1|\boldsymbol x)=\sigma(z)=\sigma(\boldsymbol{w}\cdot\boldsymbol x+b)\\ \sigma(z)=\frac{1}{1+\exp(-z)}$$

所以我们的函数集即为

$$f_{\boldsymbol {w},b}(\boldsymbol x) = P_{\boldsymbol {w},b}(C_1|\boldsymbol x)=\sigma\bigg(\sum_iw_ix_i+b\bigg)$$

此为Logistic Regression ，它与Linear Regression只相差一个 $\sigma$ 函数；Logistic Regression的输出值在0-1之间，而Linear Regression的输出值可以是任何数

Step 2：Goodness of Function

依然是最大似然估计的思想，来估计我们需要的 $\boldsymbol w$ 和 $b$

给定已知数据集的分类，上述函数 $f$ 表示当前数据属于 $C_1$ 的概率，$1-f$ 则表示属于 $C_2$ 的概率（以二分类为例）那么以当前的 $\boldsymbol w$ 和 $b$ 生成该数据集的概率为：

$$L(\boldsymbol w,b)=f(\boldsymbol x^1)f(\boldsymbol x^2)\big(1-f(\boldsymbol x^3)\big)...f(\boldsymbol x^N)$$

要找 $\boldsymbol w$ 和 $b$ 去最大化这个概率（最大似然估计标准解法，取负对数求导）

但是上面的式子形式非常的不统一，不方便后面的表述，因此对它做一下符号化，即：

$$x^i\rightarrow \hat{y}^i=\left\{\begin{matrix} 1\quad x\in C_1 \\ 0\quad x\in C_2 \end{matrix} \right.$$

那么上面的式子可以被改写为

$$\begin{align*} -\ln L(\boldsymbol w,b)=&-\ln f(\boldsymbol x^1)-\ln f(\boldsymbol x^2)-\ln \big(1-f(\boldsymbol x^3)\big)...\\ =&\sum_n-\Big[\hat{y}^n\ln(f(\boldsymbol x^n))+(1-\hat{y}^n)\ln(1-f(\boldsymbol x^n))\Big] \end{align*}$$

其实，大括号里的项就是两个伯努利分布的交叉熵（cross entropy)

假设有两个分布 p 和 q，那么他们的交叉熵定义为：$H(p,q)=-\sum_xp(x)ln(q(x))$ ，表示的含义是这两个分布有多接近，即用来衡量两个分布的相似性。如果两个分布完全一样，结果就会是 0。

Logistic Regression: 使用交叉熵判断模型的好坏 - 先验是正态

Linear Regression: 使用误差平方(square error)判断模型好坏 - 先验是二项

Step 3：Find the best function

数学推导！！！

$$\frac{\partial\Big(-\ln L(\boldsymbol w,b)\Big)}{\partial w_i}=\sum_n-[\hat{y}^n-f(\boldsymbol x^n)]x_i^n$$

括号内的项表示差距越大，更新越多

但神奇的是

Logistic Regression 的更新方式：

$$w_i\leftarrow w_i-\eta\sum_n-[\hat{y}^n-f(\boldsymbol x^n)]x_i^n$$

Linear Regression 的更新方式：

$$w_i\leftarrow w_i-\eta\sum_n-[\hat{y}^n-f(\boldsymbol x^n)]x_i^n$$

其实是一模一样的，唯一不一样的是 $\hat{y}^n$ 和 $f$ 的取值不同

为什么Logistic Regression的损失函数不用Square Error

因为 $f$ 的取值限制在了0-1之间，当估计值和目标距离很远的时候，Square Error的微分值依然很小，非常平坦，更新得很慢

但Cross Entropy在距离目标较远的地方微分值很大，更新得很快

Discriminative(判别模型) v.s. Generative(生成模型)

Discriminative: Logistic Regression => 直接找 $\boldsymbol{w}$ 和 $b$

Generative: 概率模型 => 找 $\boldsymbol{\mu}^1,\boldsymbol{\mu}^2,\boldsymbol{\Sigma}^{-1}$ => 计算 $\boldsymbol{w}$ 和 $b$ （假设了数据分布，这里是高斯分布）

两种方法找出来的w和b会一样么？（不会）=> 同样的模型，不同的方法得到了不同的方程。

生成模型的优势：

• 判别模型的准确率受训练数据量影响大，生成模型的准确率(一般来说)受训练数据量影响小。在训练数据少的情况下，通过假设数据分布提高准确率(但有时候也会适得其反)。

• 假设数据分布的做法，使生成模型对噪声数据更鲁棒

• 生成模型把参数分为 Priors probabilities 和 class-dependent probabilities，可以分别从不同的来源进行估计

  例如语音识别，现在一般使用神经网络实现（Discriminative），但事实上它是个Generative System，DNN只是其中的一部分。对语音识别来说，Priors probability指的是一句话被说出来的概率，这是不需要语音数据的，直接从网上爬文字数据就能计算出某句话出现的概率；class-dependent probability才同时需要语音和文字数据

Logistic Regression的限制

数据必须线性可分才能做。如果不能线性可分，解决方法：Feature Transformation 把原本线性不可分的特征向量转化为线性可分。但并不是所有时候都能知道如何找到一个好的Transformation方法，人找不到，那机器呢？

Cascading Logistic regression models

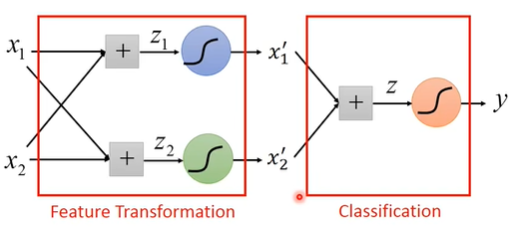
前两个logistic regression自动完成feature transformation，最后一个logistic regression完成分类

把诸多logistic regression叠加在一起，作进一步推广：

• 某个logistic regression的输入可以是其他logistic regression的输出
• 某个logistic regression的输出可以是其他logistic regression的输入

把每个logistic regression模块叫做一个Neuron，把由logistic regression组成的整体叫做Neural Network