Semi-supervised Learning

Semi-supervised Learning 半监督学习

简介

• 监督学习：全部都是labeled data
• 半监督学习：部分labeled data，部分unlabeled data，且unlabeled data数量 >> labeled data数量
  • Transductive Learning 直推学习：unlabeled data就是testing data。（测试集可以用特征，不能用label）
  • Inductive Learning 归纳推理：unlabeled data不是testing data
• 为什么进行半监督学习
  • 因为收集数据很简单，但手机labeled data很困难
  • 人类进行的就是半监督学习

半监督学习为什么有用

未标记的数据的确会告诉网络一些事情，但结果的好坏基于假设是否合理

生成模型的半监督学习

步骤

1. 初始化参数 $\theta=\{P(C_1),P(C_2),\mu^1,\mu^2,\Sigma\}$ ，已标记数据总量为 $r$ ，未标记总量为 $u$

2. 计算未标记数据的后验概率 $P_\theta(C_1|x^u)$ <— 依赖于模型参数 $\theta$

3. 更新模型：

   $$P(C_1)=\frac{N_1+\sum_{x^u}P(C_1|x^u)}{N}$$

   其中 $N$ 表示样本总数，$N_1$ 表示 $C_1$ 的样本数（labeled data），后一项表示所有未标记样本属于C1的概率和。

   $$\mu^1=\frac{1}{N_1}\sum_{x^r\in C_1}x^r+\frac{1}{\sum_{x^u}P(C_1|x^u)}\sum_{x^u}P(C_1|x^u)x^u$$

   第一项是已标记数据给的更新（平均所有属于C1的标记数据），第二项是所有未标记数据给的更新（加权平均值）

4. 重复1、2步骤直到收敛。（结果受初始值影响）

原理

• 标记数据的似然函数

  $$\ln L(\theta)=\sum_{x^r}\ln P_\theta(x^r,\hat{y}^r)\\ P_{\theta}(x^r,\hat{y}^r)=P_{\theta}(x^r|\hat{y}^r)P(\hat{y}^r)$$

• 标记数据+未标记数据的似然函数

  $$\ln L(\theta)=\sum_{x^r}\ln P_\theta(x^r,\hat{y}^r)+\sum_{x^u}\ln P_\theta(x^u)\\ P_{\theta}(x^r,\hat{y}^r)=P_{\theta}(x^r|\hat{y}^r)P(\hat{y}^r)\\ P_{\theta}(x^u)=P_{\theta}(x^u|C_1)P(C_1)+P_{\theta}(x^u|C_2)P(C_2)$$

  由于 $P_\theta(x^u)$ 不是凸函数，所以要用 EM Algorithm 迭代求解，上面的步骤1相当于E，步骤2相当于M，每更新一次，似然函数就增大一点

Low-density Separation Assumption 低密度分离假设

假设两个class的交界处密度比较低，即存在较为明显的边界

Self-training （像哪一类就是哪一类）

1. 从已标记数据中训练出一个模型 $f^*$
2. 用 $f^*$ 给未标记数据做标记 —> Pseudo-label
3. 从未标记数据集中拿出一部分数据加入已标记数据集（选择方式自定义）
4. 重复1-3步

这种方法和和半监督学习很像，不同的是，半监督学习使用的是Soft Label ，未标记数据集有部分概率属于Class 1，有部分概率属于Class 2；而Self-training使用的是Hard Label ，未标记数据要么属于Class 1，要么属于Class 2

使用Neural Network时，Soft Label 完全不起作用，只能用 Hard Label

Entropy-based Regularization (分布越集中越好)

网络输出的是一个分布，用交叉熵来判断这个分布是否集中。根据假设，分布必须是集中的

$$E(y^u)=-\sum_{m=1}^Ny_m^u\ln (y_m^u)$$

分布越集中，结果越小（越接近0）

$$L(\theta)=\sum_{x^r}C(y^r,\hat{y}^r)+\lambda\sum_{x^u}E(y^u)$$

前一项是标记数据的损失函数，后一项是未标记数据的损失函数，参数 $\lambda$ 控制两项的权重

半监督SVM

Smoothness Assumption 平滑度假设

<近朱者赤近墨者黑> $x$ 分布不均匀，如果 $x^1$ 和 $x^2$ 在一个高密度区域(high density region)很接近的话（即可以通过一条高密度的路径(high density path)相连），那么他们所对应的标签 $\hat{y}^1$ 和 $\hat{y}^2$ 是相同的。（前提：必须要能聚类在一起）

基于图的方法

将所有数据点表示成一张图上，相似度高的点相连

1. 定义两个数据间的相似度 $s(x^i,x^j)$

2. 添加边：KNN / e-Neighborhood

3. 给边增加权重，正比于相似度(RB Function: Gaussian Radial Basis Function)：

   $$s(x^i,x^j)=\exp(-\gamma||x^i-x^j||^2)$$

   选这个function的原因是，一旦 $x^i$ 和 $x^j$ 之间的距离稍微大一点，output就会下降的很快，很方便用阈值区分（数据量一定要够多）

   

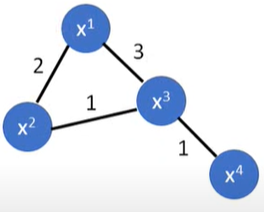
步骤

1. 定义图中所有标签的平滑度

   $$S=\frac{1}{2}\sum_{i,j}w_{i,j}(y^i-y^j)^2=\boldsymbol{y}^TL\boldsymbol{y}$$

   其中 $\boldsymbol{y}$ 是个 $(R+U)$ 维的向量，依赖于网络的参数; $L=D-W$ 是个 $(R+U)\times(R+U)$ 维的矩阵，被称为 Graph Laplacian

   矩阵 W ：按照上图建图

   矩阵 D ：一个对角矩阵，对角线上的元素为 W 每行元素之和，对角线外的元素均为0

   $$W=\begin{bmatrix}0\quad2\quad3\quad0\\2\quad0\quad1\quad0\\ 3\quad1\quad0\quad1\\0\quad0\quad1\quad0\end{bmatrix},D=\begin{bmatrix}5\quad0\quad0\quad0\\0\quad3\quad0\quad0\\ 0\quad0\quad5\quad0\\0\quad0\quad0\quad1\end{bmatrix}$$

2. 损失函数

   $$L=\sum_{x^r}C(y^r,\hat{y}^r)+\lambda S$$

   第一项是已标记数据的交叉熵函数；第二项相当于一个正则项。这个损失函数的意思是，目标网络不仅要在已标记数据上的预测结果越准确越好，同时也要保证在已标记/未标记的数据上的预测结果都要满足之前所作的 Smoothness Assumption。

   这个假设可以不只用在输出层上，也可以用在网络的任意一层

Better Representation

<化繁为简>