Tips for Deep Learning

设计网络架构和损失函数 => 得到一个Neural Network
训练集上的准确率较高，继续3；否则回到1，修改网络（欠拟合[参数过少，能力不足]或者单纯的没有训练好）
测试集上的准确率较高，结束；否则回到1，减少参数数量或修改网络（过拟合）

不同的方法针对不同的问题，是训练集准确率就低？还是训练集准确率高但测试集准确率低？

———> dropout：测试集准确率低的时候使用

Bad Results on Training Data

新的激活函数（New Activation Function）

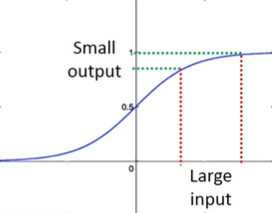
80s：sigmoid函数。深度越深，表现并不会越好。

失效原因：梯度消失

现象：靠近输入层的几层梯度较小，靠近输出层的几层梯度较大。当设定相同学习率时，前面学得很慢，后面学得很快。这会导致当前面几层还在变化的时候，后面已经收敛了，从而导致损失函数（交叉熵的和）降低得很慢，让人误以为卡在局部极小值而暂停训练。

原因：sigmoid函数会把输入的大变化衰减掉，深度越深，衰减越厉害，到输出的时候几乎没有影响了，所以越靠近输入层，对Cross Entropy的梯度越小

解决：ReLU
Rectified Linear Unit（ReLU）

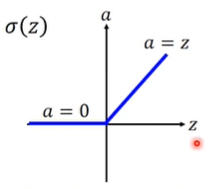
原因：1）计算速度快 2）生物学原因 3）相当于无穷多个sigmoid函数叠加的结果（bias不同）4）可以解决梯度消失的问题

输出为0的neuron对整个网络毫无影响，可以直接拿掉；而剩下的neuron满足输出=输入，所以整个网络可以看作一个瘦长的线性网络。

sigmoid函数的问题在于会把较大的输入变成较小的输出；而ReLU满足输出=输入，就不用再担心衰减的问题了。
- 但这并不是说使用ReLU激活的网络就是线性网络了，它依然是个非线性的网络（局部线性，整体非线性）
  
  当每个神经元操作数的作用域一样的时候，是线性的。也就是说，如果只对输入作小改变，而不改变神经元操作数的作用域，这时是线性的；但当对输入作大改变，从而改变了神经元操作数的作用域，就变成非线性了。 ——李宏毅
  
  ReLU的非线性体现在对不同的样本呈现出不同的状态（不同的参数）
  
  对输入样本 $\boldsymbol{x}^1$ ，网络中所有的ReLU对它都有一个确定的状态，整个网络最终对 $\boldsymbol{x}^1$ 的映射等效于一个线性映射：$\boldsymbol{y}^1=\boldsymbol{w}^1\boldsymbol{x}^1+b^1$
  
  而对另一个输入样本 $\boldsymbol{x}^2$ ，其特征与样本 $\boldsymbol{x}^1$ 不同，所以网络中的某些ReLU的激活状态因为输入变化可能发生变化，比如一些以前在右侧接通区域的变到左侧切断区域（或反之）。这样整个网络对 $\boldsymbol{x}^2$ 的映射等效于一个新的线性映射：$\boldsymbol{y}^2=\boldsymbol{w}^2\boldsymbol{x}^2+b_2$
  
  两个函数都是线性的，但参数不同，也就是说某种线性映射参数所定义的一个超平面只在某个样本附近才能成立，一旦稍微远离就会导致至少一个ReLU翻转，那么网络将有可能拟合出另一个不同参数的超平面。即不同作用域上的非线性 。 ——知乎用户 · 摩尔
- 在0处不可微：实际应用上不会恰好到这个点的
- ReLU变形
  - Leaky ReLU：$a=0.01z\quad (z<0)$
  - Parametric ReLU：$a=\alpha z\quad (z<0)$ 其中，参数 $\alpha$ 可以通过gradient descent学出来
Maxout Network
- 一个用来学习激活函数的网络，产生的激活函数是个分段线性函数（ReLU是一种特殊的由Maxout产生的激活函数）
- 概念
  
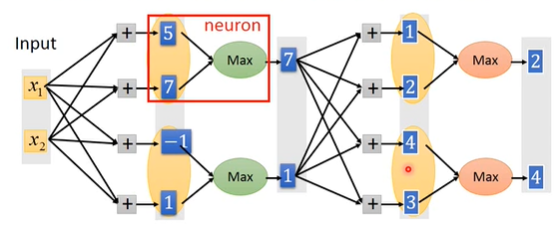
  至于几个元素一组是由人为事先决定的，从而决定了形成的激活函数由几段线性函数组成
- 怎么训练
  
  对各组中最大的元素来说，输入=输出，即梯度为1；而其他较小的元素则对网络不产生任何影响，同样可以拿掉，从而又可以将网络视为一个瘦长的线性网络。而对不同的输入样本，这种线性关系是不同的，当输入样本很多的时候，网络上的每个参数都能被训练到（这里的理解和ReLU一样）

自适应学习率（Adaptive Learning Rate）

Adagrad
$\boldsymbol{w}^{t+1}\leftarrow\boldsymbol{w}^t-\frac{\eta}{\sqrt{\sum_{i=1}^n(\boldsymbol{g}^i)^2}}\boldsymbol{g}^t$
陡峭大学习率，平缓小学习率

问题：单方向学习率不变
RMSProp
$\boldsymbol{w}^1\leftarrow\boldsymbol{w}^0-\frac{\eta}{\sigma^0}\boldsymbol{g}^0\qquad \sigma^0=\boldsymbol{g}^0\\ \boldsymbol{w}^2\leftarrow\boldsymbol{w}^1-\frac{\eta}{\sigma^1}\boldsymbol{g}^1\qquad \sigma^1=\sqrt{\alpha(\sigma^0)^2+(1-\alpha)(\boldsymbol{g}^1)^2}\\ \boldsymbol{w}^3\leftarrow\boldsymbol{w}^2-\frac{\eta}{\sigma^2}\boldsymbol{g}^2\qquad \sigma^2=\sqrt{\alpha(\sigma^1)^2+(1-\alpha)(\boldsymbol{g}^2)^2}\\ \cdots \\ \boldsymbol{w}^{t+1}\leftarrow\boldsymbol{w}^t-\frac{\eta}{\sigma^t}\boldsymbol{g}^t\qquad \sigma^t=\sqrt{\alpha(\sigma^{t-1})^2+(1-\alpha)(\boldsymbol{g}^t)^2}$
虽然同样在算梯度的均方根（Root Mean Square），但可以给新看到的梯度比较大的权重，给过去看到的梯度比较小的梯度，从而解决Adagrad同方向学习率不变的问题。
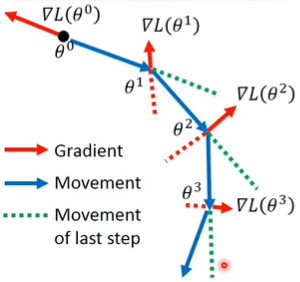
Momentum

除了当前的梯度，还参考了当前的惯性，也就是把之前的梯度也纳入考虑，越远的梯度系数越小，参考影响越小；越近的梯度参考影响越大。这种方法在某些时候可以帮助跳出局部极小值点。

Position	Movement	Gradient
$\boldsymbol{\theta}^0$	$\boldsymbol{v}^0=0$	$\nabla L(\boldsymbol{\theta}^0)$
$\boldsymbol{\theta}^1=\boldsymbol{\theta}^0+\boldsymbol{v}^1$	$\boldsymbol{v}^1=\lambda\boldsymbol{v}^0-\eta\nabla L(\boldsymbol{\theta}^0)=-\eta\nabla L(\boldsymbol{\theta}^0)$	$\nabla L(\boldsymbol{\theta}^1)$
$\boldsymbol{\theta}^2=\boldsymbol{\theta}^1+\boldsymbol{v}^2$	$\boldsymbol{v}^2=\lambda\boldsymbol{v}^1-\eta\nabla L(\boldsymbol{\theta}^1)=-\lambda \eta\nabla L(\boldsymbol{\theta}^0)-\eta\nabla L(\boldsymbol{\theta}^1)$	$\nabla L(\boldsymbol{\theta}^2)$

Adam = RMSprop + Momentum

Bad Results on Testing Data

早点停

正则化 Regularization

重新定义一个损失函数，在原损失函数的基础上加上正则项（以2-norm为例）：

$L'(\theta)=L(\theta)+\lambda\frac{1}{2}||\theta||_2\\ ||\theta||_2=\sum_{i=1}^n(w_i)^2 \\ \frac{\partial L'}{\partial w}=\frac{\partial L}{\partial w}+\lambda w \\ w^{t+1}\leftarrow w^t-\eta\frac{\partial L'}{\partial w}=(1-\eta\lambda)w^t-\eta\frac{\partial L}{\partial w}$

正则化一般不考虑 bias 项，因为正则化的目的是让function变得平滑，而bias与function的平滑程度没有关系。

$(1-\eta\lambda)$ 非常接近1，使得 $(1-\eta\lambda)w^t$ 越来越接近0，而后面的微分项保证了整体不会都变成0。

L1和L2的区别：L1的结果很稀疏，会有接近0的点，也会有离0远的点；L2的结果基本都是集中在0附近较小的点

Weight Decay：每次都让weight小一点

目的：参数不要离0太远。（和早点停的作用很像）

Dropout

怎么做

训练时：每次更新参数前，对神经元作采样（包括输入），神经元有p%的几率被丢掉，相连的weight也会相应地被丢掉，所以每次更新时的网络结构都是不同的，并且在训练集上的表现会变差（所以如果训练集本身训练效果就不是很好，就不能加dropout来解决）

测试时：
1. 不做dropout
2. 如果训练时的dropout rate=p%，那么测试的时候，所有weight都要乘上 (1-p%) .
为什么有用

终极Ensemble方法。一个复杂网络往往bias小，但variance很大。通过训练很多个这样的复杂网络，将数据经过所有网络后的输出平均（这与所有weight都乘上(1-p%)等效），这样variance也会得到平均，结果就会比较准。网络越接近线性网络，效果越好。