Unsupervised Learning-Linear Methods

Unsupervised Learning-Linear Methods

• Clustering & Dimension Reduction — 化繁为简（不同的input，相同的抽象output）只有输入数据
• Generation — 无中生有（不同input，不同output）只有输出数据

Clustering

• K-means（需要先知道聚类数）

  1. 初始化聚类中心（随机K个）
  2. 对所有数据，计算到它距离最近的聚类中心
  3. 更新聚类中心（做平均）
  4. 重复2-3步

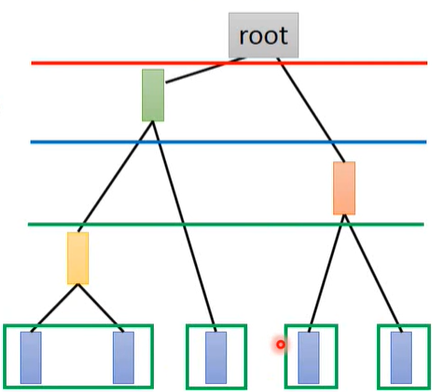
• Hierarchical Agglomerative Clustering（HAC - 层次聚类，不用事先决定聚类数）

  1. 建树。找相似度最近的两组数据取平均得到一个新的数据

  2. 选阈值。划分cluster

     

• Distributed Representation

  用一个vector来表示对象，每一维都表示某种特征(attribute)的占比；而不是只划分为某个cluster，这样会丢掉一些有用信息

• Dimension Reduction

  通过Distributed Representation把高维信息(例如图像)变到低维空间

  • Feature Selection

  • Principle Component Analysis（PCA 主成分分析）

    PCA是一种常用的降维方法，输入数据 $\boldsymbol{x}$ ，输出数据 $\boldsymbol{z}$ ，后者的维度比前者小，且满足 $\boldsymbol{z}=\boldsymbol{W}\boldsymbol{x}$ 。目的就是为了找到这个W。以一维数据为例（即取向量z的第一个数据）W的第一行，显然有：

    $$z_1=\boldsymbol{w}^1\cdot \boldsymbol{x}$$

    假设 $||\boldsymbol{w}^1||_2=1$ ，内积 $z_1$ 的几何意义是 $\boldsymbol{x}$ 在 $\boldsymbol{w}^1$ 上的投影长度。PCA要做的事就是将所有数据点 x 投影到 $\boldsymbol{w}^1$ 上，得到一个 $z_1$ 的集合，并且这个集合元素的方差（variance）越大越好（最大限度保留数据点的区别度）：

    $$Var(z_1)=\sum_{z_1}(z_1-\bar{z_1})^2$$

    以上是投影到一维平面，如果投影到二维平面，则同样还有：

    $$Var(z_2)=\sum_{z_2}(z_2-\bar{z_2})^2\quad||\boldsymbol{w}^2||_2=1$$

    在保证 Var 越大越好的情况下(拉格朗日)，还要保证 $\boldsymbol{w}^1\cdot\boldsymbol{w}^2=0$ ，即两个向量垂直

    同样的方法处理K维。因此找出来的矩阵W是个orthogonal matrix。根据 $(a\cdot b)^2=(a\cdot b)(b\cdot a)=a^Tbb^Ta$ 对（2）作化简：

    $$\bar{z_1}=\frac{1}{n}\sum z_1=\frac{1}{n}\sum w^1\cdot x=w^1\cdot \frac{1}{n}\sum x=w^1\cdot\bar{x}\\ \begin{align} \begin{split} Var(z_1)&=\sum_{z_1}(z_1-\bar{z_1})^2\\ &=\sum_{x}(w^1\cdot x-w^1\cdot\bar{x})^2\\ &=\sum_{x}(w^1\cdot(x-\bar{x}))^2\\ &=\sum_{x}(w^1)^T(x-\bar{x})(x-\bar{x})^Tw^1\\ &=(w^1)^T{\color{blue}\sum(x-\bar{x})(x-\bar{x})^T}w^1\\ &=(w^1)^T{\color{blue}Cov(x)} w^1 \\ &\triangleq (w^1)^T{\color{blue}S}w^1 \end{split} \end{align}$$

    问题转化成：

    Ⅰ

    找到一个 $\boldsymbol{w}^1$ 满足 $||\boldsymbol{w}^1||_2=(\boldsymbol{w}^1)^T\boldsymbol{w}^1=1$ ，使得 $(\boldsymbol{w}^1)^T S \boldsymbol{w}^1$ 最大。

    由于$S=Cov(x)$ ，所以它是一个半正定(所有特征值非负)的对称矩阵。

    结论：这个 $\boldsymbol{w}^1$ 是协方差矩阵 $S$ 最大特征值所对应的特征向量（证明方法：拉格朗日乘数法）

    $$g(\boldsymbol{w}^1)=(\boldsymbol{w}^1)^TS\boldsymbol{w}^1-\alpha((\boldsymbol{w}^1)^T\boldsymbol{w}^1-1)$$

    对 $\boldsymbol{w}^1$ 的每一项 $w^1_i$ 求偏微分将会得到：

    $$S\boldsymbol{w}^1-\alpha\boldsymbol{w}^1=0\Rightarrow S\boldsymbol{w}^1=\alpha \boldsymbol{w}^1$$

    带入目标函数：

    $$(\boldsymbol{w}^1)^TS\boldsymbol{w}^1=\alpha(\boldsymbol{w}^1)^T\boldsymbol{w}^1=\alpha$$

    结论显然

    Ⅱ

    找到一个 $\boldsymbol{w}^2$ 满足 $||\boldsymbol{w}^2||_2=(\boldsymbol{w}^2)^T\boldsymbol{w}^2=1$ 且 $(\boldsymbol{w}^2)^T\boldsymbol{w}^1=0$ ，使得 $(\boldsymbol{w}^2)^T S \boldsymbol{w}^2$ 最大。

    结论：这个 $\boldsymbol{w}^2$ 是协方差矩阵 $S$ 第二大特征值所对应的特征向量（证明方法：拉格朗日乘数法，证明略）

    PCA去关联后的数据$z$的均方差矩阵是个对角阵 —— z 是一种新的特征，给其他模型用的时候，就可以直接假设不同维度间相关系数为0，从而大大减少参数量，从而避免过拟合情况

    $$\begin{align} \begin{split} Cov(z)&=\sum(z-\bar{z})(z-\bar{z})^T=WSW^T\\ &=WS[w^1\dots w^K]\\ &=W[Sw^1\dots Sw^K]\\ &=W[\lambda_1w^1\dots \lambda_Kw^K]\\ &=[\lambda_1Ww^1\dots \lambda_KWw^K]\\ &=[\lambda_1e^1\dots \lambda_Ke^K]=D \end{split} \end{align}$$
    • 从另外的角度看PCA

    用若干component来描述一张image：

    $$\boldsymbol{x}-\bar{\boldsymbol{x}}\approx c_1\boldsymbol{u}^1+c_2\boldsymbol{u}^2+\dots+c_K\boldsymbol{u}^K=\hat{\boldsymbol{x}}$$

    但这些component是未知的，现在需要找出这K个component，使得左边最接近右边，即最小化Reconstruction Error：

    $$L=\min_{\{u^1,\dots u^K\}}||(x-\bar{x})-\hat{x}||_2=\min_{\{u^1,\dots u^K\}}||(x-\bar{x})-\Big(\sum_{k=1}^Kc_ku^k \Big)||_2$$

    事实上，由上面PCA求解出的 $w^i$ 其实就是上式的解（SVD分解）

    如何确定系数 $c_i$ ？

    由上可知，$u^i$ 本质上就是相互正交的 $w^i$ ，现在需要找到一组系数 $c_i$ 使得上式最小，根据正交性，乘上 $w^k$ 后：

    $$w^kL=\min_{\{c_1,\dots,c_k\}}||(x-\bar{x})\cdot w^k-c_k||$$

    显然，当 $c_k=(x-\bar{x})\cdot w^k$ 的时候上式最小（等于0）

    • PCA 与 Neural Network 的关系

    PCA ≈ 有一层隐藏层（线性激活函数）的神经网络 <== 自动编码器 Autoencoder

    

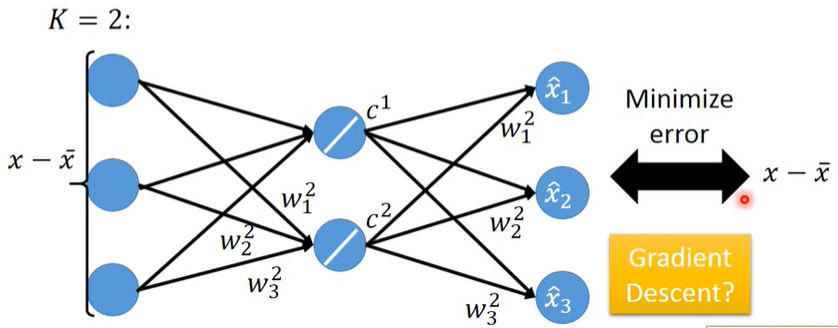
    直接用GD解出的weight不能保证相互正交，不能让Reconstruction Error最小

    在线性条件下，NN的方法会比PCA更麻烦一些，且更不精确一些。

    但用神经网络的优势在于，它可以变深 ==> Deep Autoencoder

    • PCA的缺点

    非监督的（容易混淆不同类别的数据），线性的（不能执行非线性的变换）

    求出的系数可能是负值（NMF解决）

    • Matrix Factorization（应用 Topic Analysis）