潘薇鸿

Unsupervised Learning: Neighbor Embedding

非线性降维

Manifold Learning（流形学习）

• 高维曲面空间降维到低维（例如二维）空间，使得欧氏几何关系成立

  

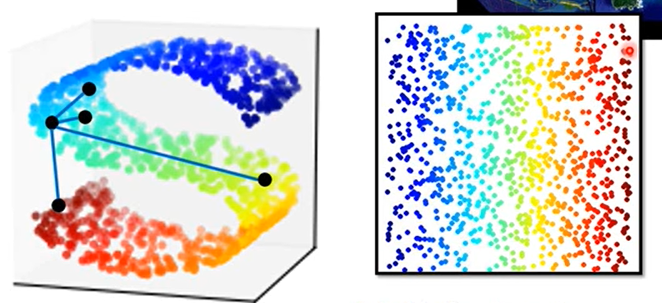
Locally Linear Embedding（LLE）

• 用 $w_{ij}$ 表示空间两点 $x^i$ 和 $x^j$ 之间的关系。$x^i$ 可以由周围的点做加权和表示出来

• 找一组 $w_{ij}$ 最小化：

  $$\sum_i||x^i-\sum_jw_{ij}x^j||_2$$

• 根据 $w_{ij}$ 将 $x_i$ 、$x_j$ 转化为 $z_i$ 、$z_j$

  • 保持 $w_{ij}$ 不变，找到一组低维向量 $z^i$ 最小化： $$\sum_i||z^i-\sum_jw_{ij}z^j||_2$$

• 选取neighbor的个数会对最终结果产生一定影响，太大太小都不行

Laplacian Eigenmaps

• Graph-based approach

Unsupervised Learning: Word Embedding

生成词向量是个非监督的过程，只有输入数据而不知道输出数据

这个问题不能用Auto-encoder来解（1-of-N encoding之间没有体现出词汇间的关联性）

Word Embedding

机器通过上下文学习一个单词的意思

Count based

• 如果两个单词经常同时出现，那么这两个单词的词向量彼此接近

Prediction based

• 给神经网络一个单词，预测下一个可能出现的单词（每个单词出现的机率）

• 用第一层的neurons代表一个单词：词向量(word vector)/词嵌入特征(word embedding feature) —> V(w)

• Sharing Parameters : 当用多个单词预测下一个单词的时候，同维对应的权重 $w_i$、$w_j$ 相同

  

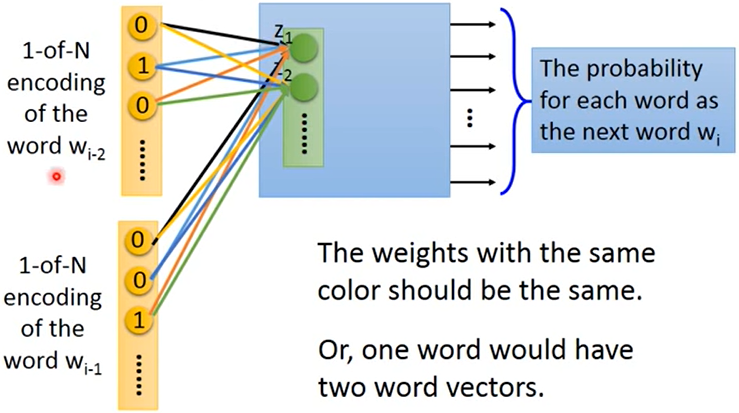
  • 为什么：如果不这么做，交换单词的输入顺序将会得到不同的结果；可以减少参数量

  • 怎么做：

    • 给 $w_i$ 和 $w_j$ 相同的初始值

    • 更新

      $$w_i\leftarrow w_i-\eta \frac{\partial C}{\partial w_i}-\eta\frac{\partial C}{\partial w_j}\\ w_j\leftarrow w_j-\eta \frac{\partial C}{\partial w_j}-\eta\frac{\partial C}{\partial w_i}$$

• Training : 最小化输出和目标词汇的交叉熵

• 不同的架构

  • Continuous bag of word(CBOW) model：用上下文来预测中间可能出现的词汇
  • Skip-gram：用中间的词汇预测上下文可能出现的词汇

其他应用

• Multi-lingual Embedding
• Multi-domain Embedding
• Semantic Embedding (document —> vector)
  • 只用BOW描述一篇文章是远不够的（语序不同导致的意义不同）

Unsupervised Learning-Linear Methods

• Clustering & Dimension Reduction — 化繁为简（不同的input，相同的抽象output）只有输入数据
• Generation — 无中生有（不同input，不同output）只有输出数据

Clustering

• K-means（需要先知道聚类数）

  1. 初始化聚类中心（随机K个）
  2. 对所有数据，计算到它距离最近的聚类中心
  3. 更新聚类中心（做平均）
  4. 重复2-3步

• Hierarchical Agglomerative Clustering（HAC - 层次聚类，不用事先决定聚类数）

  1. 建树。找相似度最近的两组数据取平均得到一个新的数据

  2. 选阈值。划分cluster

     

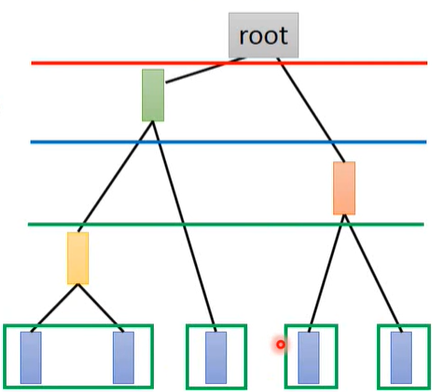
• Distributed Representation

  用一个vector来表示对象，每一维都表示某种特征(attribute)的占比；而不是只划分为某个cluster，这样会丢掉一些有用信息

• Dimension Reduction

  通过Distributed Representation把高维信息(例如图像)变到低维空间

  • Feature Selection

  • Principle Component Analysis（PCA 主成分分析）

    PCA是一种常用的降维方法，输入数据 $\boldsymbol{x}$ ，输出数据 $\boldsymbol{z}$ ，后者的维度比前者小，且满足 $\boldsymbol{z}=\boldsymbol{W}\boldsymbol{x}$ 。目的就是为了找到这个W。以一维数据为例（即取向量z的第一个数据）W的第一行，显然有：

    $$z_1=\boldsymbol{w}^1\cdot \boldsymbol{x}$$

    假设 $||\boldsymbol{w}^1||_2=1$ ，内积 $z_1$ 的几何意义是 $\boldsymbol{x}$ 在 $\boldsymbol{w}^1$ 上的投影长度。PCA要做的事就是将所有数据点 x 投影到 $\boldsymbol{w}^1$ 上，得到一个 $z_1$ 的集合，并且这个集合元素的方差（variance）越大越好（最大限度保留数据点的区别度）：

    $$Var(z_1)=\sum_{z_1}(z_1-\bar{z_1})^2$$

    以上是投影到一维平面，如果投影到二维平面，则同样还有：

    $$Var(z_2)=\sum_{z_2}(z_2-\bar{z_2})^2\quad||\boldsymbol{w}^2||_2=1$$

    在保证 Var 越大越好的情况下(拉格朗日)，还要保证 $\boldsymbol{w}^1\cdot\boldsymbol{w}^2=0$ ，即两个向量垂直

    同样的方法处理K维。因此找出来的矩阵W是个orthogonal matrix。根据 $(a\cdot b)^2=(a\cdot b)(b\cdot a)=a^Tbb^Ta$ 对（2）作化简：

    $$\bar{z_1}=\frac{1}{n}\sum z_1=\frac{1}{n}\sum w^1\cdot x=w^1\cdot \frac{1}{n}\sum x=w^1\cdot\bar{x}\\ \begin{align} \begin{split} Var(z_1)&=\sum_{z_1}(z_1-\bar{z_1})^2\\ &=\sum_{x}(w^1\cdot x-w^1\cdot\bar{x})^2\\ &=\sum_{x}(w^1\cdot(x-\bar{x}))^2\\ &=\sum_{x}(w^1)^T(x-\bar{x})(x-\bar{x})^Tw^1\\ &=(w^1)^T{\color{blue}\sum(x-\bar{x})(x-\bar{x})^T}w^1\\ &=(w^1)^T{\color{blue}Cov(x)} w^1 \\ &\triangleq (w^1)^T{\color{blue}S}w^1 \end{split} \end{align}$$

    问题转化成：

    Ⅰ

    找到一个 $\boldsymbol{w}^1$ 满足 $||\boldsymbol{w}^1||_2=(\boldsymbol{w}^1)^T\boldsymbol{w}^1=1$ ，使得 $(\boldsymbol{w}^1)^T S \boldsymbol{w}^1$ 最大。

    由于$S=Cov(x)$ ，所以它是一个半正定(所有特征值非负)的对称矩阵。

    结论：这个 $\boldsymbol{w}^1$ 是协方差矩阵 $S$ 最大特征值所对应的特征向量（证明方法：拉格朗日乘数法）

    $$g(\boldsymbol{w}^1)=(\boldsymbol{w}^1)^TS\boldsymbol{w}^1-\alpha((\boldsymbol{w}^1)^T\boldsymbol{w}^1-1)$$

    对 $\boldsymbol{w}^1$ 的每一项 $w^1_i$ 求偏微分将会得到：

    $$S\boldsymbol{w}^1-\alpha\boldsymbol{w}^1=0\Rightarrow S\boldsymbol{w}^1=\alpha \boldsymbol{w}^1$$

    带入目标函数：

    $$(\boldsymbol{w}^1)^TS\boldsymbol{w}^1=\alpha(\boldsymbol{w}^1)^T\boldsymbol{w}^1=\alpha$$

    结论显然

    Ⅱ

    找到一个 $\boldsymbol{w}^2$ 满足 $||\boldsymbol{w}^2||_2=(\boldsymbol{w}^2)^T\boldsymbol{w}^2=1$ 且 $(\boldsymbol{w}^2)^T\boldsymbol{w}^1=0$ ，使得 $(\boldsymbol{w}^2)^T S \boldsymbol{w}^2$ 最大。

    结论：这个 $\boldsymbol{w}^2$ 是协方差矩阵 $S$ 第二大特征值所对应的特征向量（证明方法：拉格朗日乘数法，证明略）

    PCA去关联后的数据$z$的均方差矩阵是个对角阵 —— z 是一种新的特征，给其他模型用的时候，就可以直接假设不同维度间相关系数为0，从而大大减少参数量，从而避免过拟合情况

    $$\begin{align} \begin{split} Cov(z)&=\sum(z-\bar{z})(z-\bar{z})^T=WSW^T\\ &=WS[w^1\dots w^K]\\ &=W[Sw^1\dots Sw^K]\\ &=W[\lambda_1w^1\dots \lambda_Kw^K]\\ &=[\lambda_1Ww^1\dots \lambda_KWw^K]\\ &=[\lambda_1e^1\dots \lambda_Ke^K]=D \end{split} \end{align}$$
    • 从另外的角度看PCA

    用若干component来描述一张image：

    $$\boldsymbol{x}-\bar{\boldsymbol{x}}\approx c_1\boldsymbol{u}^1+c_2\boldsymbol{u}^2+\dots+c_K\boldsymbol{u}^K=\hat{\boldsymbol{x}}$$

    但这些component是未知的，现在需要找出这K个component，使得左边最接近右边，即最小化Reconstruction Error：

    $$L=\min_{\{u^1,\dots u^K\}}||(x-\bar{x})-\hat{x}||_2=\min_{\{u^1,\dots u^K\}}||(x-\bar{x})-\Big(\sum_{k=1}^Kc_ku^k \Big)||_2$$

    事实上，由上面PCA求解出的 $w^i$ 其实就是上式的解（SVD分解）

    如何确定系数 $c_i$ ？

    由上可知，$u^i$ 本质上就是相互正交的 $w^i$ ，现在需要找到一组系数 $c_i$ 使得上式最小，根据正交性，乘上 $w^k$ 后：

    $$w^kL=\min_{\{c_1,\dots,c_k\}}||(x-\bar{x})\cdot w^k-c_k||$$

    显然，当 $c_k=(x-\bar{x})\cdot w^k$ 的时候上式最小（等于0）

    • PCA 与 Neural Network 的关系

    PCA ≈ 有一层隐藏层（线性激活函数）的神经网络 <== 自动编码器 Autoencoder

    

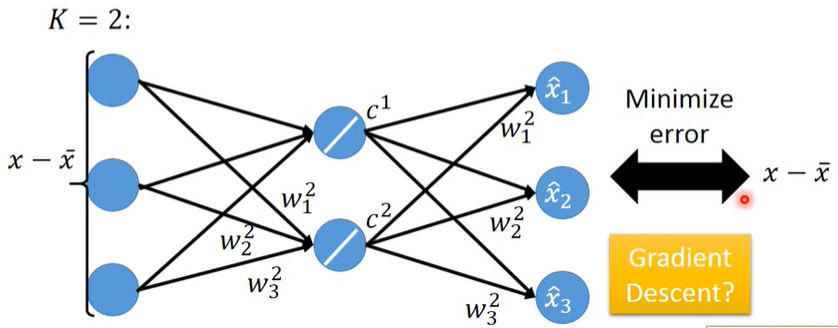
    直接用GD解出的weight不能保证相互正交，不能让Reconstruction Error最小

    在线性条件下，NN的方法会比PCA更麻烦一些，且更不精确一些。

    但用神经网络的优势在于，它可以变深 ==> Deep Autoencoder

    • PCA的缺点

    非监督的（容易混淆不同类别的数据），线性的（不能执行非线性的变换）

    求出的系数可能是负值（NMF解决）

    • Matrix Factorization（应用 Topic Analysis）

Semi-supervised Learning 半监督学习

简介

• 监督学习：全部都是labeled data
• 半监督学习：部分labeled data，部分unlabeled data，且unlabeled data数量 >> labeled data数量
  • Transductive Learning 直推学习：unlabeled data就是testing data。（测试集可以用特征，不能用label）
  • Inductive Learning 归纳推理：unlabeled data不是testing data
• 为什么进行半监督学习
  • 因为收集数据很简单，但手机labeled data很困难
  • 人类进行的就是半监督学习

半监督学习为什么有用

未标记的数据的确会告诉网络一些事情，但结果的好坏基于假设是否合理

生成模型的半监督学习

步骤

1. 初始化参数 $\theta=\{P(C_1),P(C_2),\mu^1,\mu^2,\Sigma\}$ ，已标记数据总量为 $r$ ，未标记总量为 $u$

2. 计算未标记数据的后验概率 $P_\theta(C_1|x^u)$ <— 依赖于模型参数 $\theta$

3. 更新模型：

   $$P(C_1)=\frac{N_1+\sum_{x^u}P(C_1|x^u)}{N}$$

   其中 $N$ 表示样本总数，$N_1$ 表示 $C_1$ 的样本数（labeled data），后一项表示所有未标记样本属于C1的概率和。

   $$\mu^1=\frac{1}{N_1}\sum_{x^r\in C_1}x^r+\frac{1}{\sum_{x^u}P(C_1|x^u)}\sum_{x^u}P(C_1|x^u)x^u$$

   第一项是已标记数据给的更新（平均所有属于C1的标记数据），第二项是所有未标记数据给的更新（加权平均值）

4. 重复1、2步骤直到收敛。（结果受初始值影响）

原理

• 标记数据的似然函数

  $$\ln L(\theta)=\sum_{x^r}\ln P_\theta(x^r,\hat{y}^r)\\ P_{\theta}(x^r,\hat{y}^r)=P_{\theta}(x^r|\hat{y}^r)P(\hat{y}^r)$$

• 标记数据+未标记数据的似然函数

  $$\ln L(\theta)=\sum_{x^r}\ln P_\theta(x^r,\hat{y}^r)+\sum_{x^u}\ln P_\theta(x^u)\\ P_{\theta}(x^r,\hat{y}^r)=P_{\theta}(x^r|\hat{y}^r)P(\hat{y}^r)\\ P_{\theta}(x^u)=P_{\theta}(x^u|C_1)P(C_1)+P_{\theta}(x^u|C_2)P(C_2)$$

  由于 $P_\theta(x^u)$ 不是凸函数，所以要用 EM Algorithm 迭代求解，上面的步骤1相当于E，步骤2相当于M，每更新一次，似然函数就增大一点

Low-density Separation Assumption 低密度分离假设

假设两个class的交界处密度比较低，即存在较为明显的边界

Self-training （像哪一类就是哪一类）

1. 从已标记数据中训练出一个模型 $f^*$
2. 用 $f^*$ 给未标记数据做标记 —> Pseudo-label
3. 从未标记数据集中拿出一部分数据加入已标记数据集（选择方式自定义）
4. 重复1-3步

这种方法和和半监督学习很像，不同的是，半监督学习使用的是Soft Label ，未标记数据集有部分概率属于Class 1，有部分概率属于Class 2；而Self-training使用的是Hard Label ，未标记数据要么属于Class 1，要么属于Class 2

使用Neural Network时，Soft Label 完全不起作用，只能用 Hard Label

Entropy-based Regularization (分布越集中越好)

网络输出的是一个分布，用交叉熵来判断这个分布是否集中。根据假设，分布必须是集中的

$$E(y^u)=-\sum_{m=1}^Ny_m^u\ln (y_m^u)$$

分布越集中，结果越小（越接近0）

$$L(\theta)=\sum_{x^r}C(y^r,\hat{y}^r)+\lambda\sum_{x^u}E(y^u)$$

前一项是标记数据的损失函数，后一项是未标记数据的损失函数，参数 $\lambda$ 控制两项的权重

半监督SVM

Smoothness Assumption 平滑度假设

<近朱者赤近墨者黑> $x$ 分布不均匀，如果 $x^1$ 和 $x^2$ 在一个高密度区域(high density region)很接近的话（即可以通过一条高密度的路径(high density path)相连），那么他们所对应的标签 $\hat{y}^1$ 和 $\hat{y}^2$ 是相同的。（前提：必须要能聚类在一起）

基于图的方法

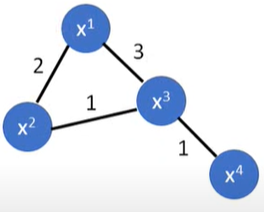
将所有数据点表示成一张图上，相似度高的点相连

1. 定义两个数据间的相似度 $s(x^i,x^j)$

2. 添加边：KNN / e-Neighborhood

3. 给边增加权重，正比于相似度(RB Function: Gaussian Radial Basis Function)：

   $$s(x^i,x^j)=\exp(-\gamma||x^i-x^j||^2)$$

   选这个function的原因是，一旦 $x^i$ 和 $x^j$ 之间的距离稍微大一点，output就会下降的很快，很方便用阈值区分（数据量一定要够多）

   

步骤

1. 定义图中所有标签的平滑度

   $$S=\frac{1}{2}\sum_{i,j}w_{i,j}(y^i-y^j)^2=\boldsymbol{y}^TL\boldsymbol{y}$$

   其中 $\boldsymbol{y}$ 是个 $(R+U)$ 维的向量，依赖于网络的参数; $L=D-W$ 是个 $(R+U)\times(R+U)$ 维的矩阵，被称为 Graph Laplacian

   矩阵 W ：按照上图建图

   矩阵 D ：一个对角矩阵，对角线上的元素为 W 每行元素之和，对角线外的元素均为0

   $$W=\begin{bmatrix}0\quad2\quad3\quad0\\2\quad0\quad1\quad0\\ 3\quad1\quad0\quad1\\0\quad0\quad1\quad0\end{bmatrix},D=\begin{bmatrix}5\quad0\quad0\quad0\\0\quad3\quad0\quad0\\ 0\quad0\quad5\quad0\\0\quad0\quad0\quad1\end{bmatrix}$$

2. 损失函数

   $$L=\sum_{x^r}C(y^r,\hat{y}^r)+\lambda S$$

   第一项是已标记数据的交叉熵函数；第二项相当于一个正则项。这个损失函数的意思是，目标网络不仅要在已标记数据上的预测结果越准确越好，同时也要保证在已标记/未标记的数据上的预测结果都要满足之前所作的 Smoothness Assumption。

   这个假设可以不只用在输出层上，也可以用在网络的任意一层

Better Representation

<化繁为简>

卷积神经网络

CNN做了什么

如果只用Fully Connected Neural Network，会导致参数数量巨大；CNN所做的就是通过考虑图像特征（先验知识）来简化网络。复杂又简单

为什么可以用较少的参数完成图像识别

1. 某个神经元是为了检测某种特征，所以它不需要看完整张图，而只需要看图像的一小部分。所以每个神经元只需要和一个小区域形成联系。（Convolution Layer 实现）
2. 同样的特征可能出现在不同的区域，这个“位置”信息是冗余的，所以在不同位置的相同特征可以共享同一组参数。（Convolution Layer 实现）
3. 对图像作降采样不会影响图像识别的结果，通过降低图片大小可以减少网络所需要的参数。（Max Pooling Layer 实现）

CNN架构

Input Image —> repeat (Convolution + Max Pooling) for several times —> Flatten —> FCN (Fully Connected Network) —> result

Convolution

一个卷积层可以有很多个filter，相当于很多个神经元，每个filter提取一种局部特征。

由这些filter分别和原图作卷积，输出图像叠起来就是 Feature Map

卷积和全连接的联系

把卷积的输入图像拉成一个一维向量，filter的移动相当于表示每次选取哪些维度作计算，filter中的每个数值相当于weight，由于filter是固定的，所以每次计算输出时所用的weight是相同的，即Shared Weights，这样就可以实现用较少的参数实现特征提取的结果。

Max Pooling

作下采样。把输出的 Feature Map 中每一层2$\times$2的value取平均/取最大保留下来，从而实现降维

输出深度（channel）由filter总数决定，几个filter就有几个输出channel

Flatten+FCN

把输出的 Feature Map 拉直成一个一维向量扔到FCN里

怎么分析CNN学到了什么？

卷积层

设某个卷积层的第k个filter的输出是一个11$\times$11的矩阵

定义第k个filter的激活度，激活度越高，这一部分的特征越接近第k个filter所表示的特征：

$$a^k=\sum_{i=1}^{11}\sum_{j=1}^{11}a^k_{ij}$$

所以，要想知道第k个filter学习到的是什么特征，也就是找一个输入图像 $x^*$ ，使得：

$$x^*=arg\max_{x}a^k$$

找最大值用 Gradient Ascent

FCN层

设FCN的每个神经元的输出是 $a^j$ ，现在要做的事找一个图像去最大化这个输出，也就是：

$$x^*=arg\max_{x}a^j$$

对输出层也是如此。但稍微不同的是，会根据先前的输入输出先验限制条件为它加条件：

$$x^*=arg\max_x\Big(y^i-\sum_{i,j}|x_{ij}|\Big)$$

这只是个举例

Tips for Deep Learning

1. 设计网络架构和损失函数 => 得到一个Neural Network
2. 训练集上的准确率较高，继续3；否则回到1，修改网络（欠拟合[参数过少，能力不足]或者单纯的没有训练好）
3. 测试集上的准确率较高，结束；否则回到1，减少参数数量或修改网络（过拟合）

不同的方法针对不同的问题，是训练集准确率就低？还是训练集准确率高但测试集准确率低？

———> dropout：测试集准确率低的时候使用

Bad Results on Training Data

新的激活函数（New Activation Function）

• 80s：sigmoid函数。深度越深，表现并不会越好。

  失效原因：梯度消失

  现象：靠近输入层的几层梯度较小，靠近输出层的几层梯度较大。当设定相同学习率时，前面学得很慢，后面学得很快。这会导致当前面几层还在变化的时候，后面已经收敛了，从而导致损失函数（交叉熵的和）降低得很慢，让人误以为卡在局部极小值而暂停训练。

  原因：sigmoid函数会把输入的大变化衰减掉，深度越深，衰减越厉害，到输出的时候几乎没有影响了，所以越靠近输入层，对Cross Entropy的梯度越小

  

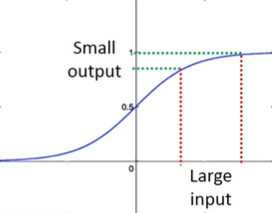
  解决：ReLU

• Rectified Linear Unit（ReLU）

  

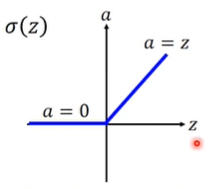
  原因：1）计算速度快 2）生物学原因 3）相当于无穷多个sigmoid函数叠加的结果（bias不同）4）可以解决梯度消失的问题

  输出为0的neuron对整个网络毫无影响，可以直接拿掉；而剩下的neuron满足输出=输入，所以整个网络可以看作一个瘦长的线性网络。

  sigmoid函数的问题在于会把较大的输入变成较小的输出；而ReLU满足输出=输入，就不用再担心衰减的问题了。

  • 但这并不是说使用ReLU激活的网络就是线性网络了，它依然是个非线性的网络（局部线性，整体非线性）

    当每个神经元操作数的作用域一样的时候，是线性的。也就是说，如果只对输入作小改变，而不改变神经元操作数的作用域，这时是线性的；但当对输入作大改变，从而改变了神经元操作数的作用域，就变成非线性了。 ——李宏毅

    ReLU的非线性体现在对不同的样本呈现出不同的状态（不同的参数）

    对输入样本 $\boldsymbol{x}^1$ ，网络中所有的ReLU对它都有一个确定的状态，整个网络最终对 $\boldsymbol{x}^1$ 的映射等效于一个线性映射：$\boldsymbol{y}^1=\boldsymbol{w}^1\boldsymbol{x}^1+b^1$

    而对另一个输入样本 $\boldsymbol{x}^2$ ，其特征与样本 $\boldsymbol{x}^1$ 不同，所以网络中的某些ReLU的激活状态因为输入变化可能发生变化，比如一些以前在右侧接通区域的变到左侧切断区域（或反之）。这样整个网络对 $\boldsymbol{x}^2$ 的映射等效于一个新的线性映射：$\boldsymbol{y}^2=\boldsymbol{w}^2\boldsymbol{x}^2+b_2$

    两个函数都是线性的，但参数不同，也就是说某种线性映射参数所定义的一个超平面只在某个样本附近才能成立，一旦稍微远离就会导致至少一个ReLU翻转，那么网络将有可能拟合出另一个不同参数的超平面。即不同作用域上的非线性 。 ——知乎用户 · 摩尔

  • 在0处不可微：实际应用上不会恰好到这个点的

  • ReLU变形

    • Leaky ReLU：$a=0.01z\quad (z<0)$
    • Parametric ReLU：$a=\alpha z\quad (z<0)$ 其中，参数 $\alpha$ 可以通过gradient descent学出来

• Maxout Network

  • 一个用来学习激活函数的网络，产生的激活函数是个分段线性函数（ReLU是一种特殊的由Maxout产生的激活函数）

  • 概念

    

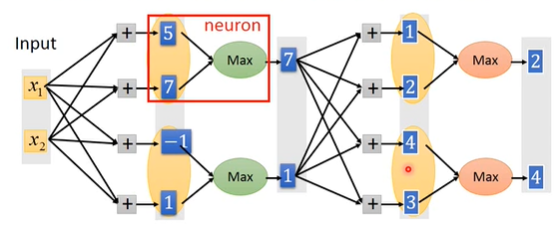
    至于几个元素一组是由人为事先决定的，从而决定了形成的激活函数由几段线性函数组成

  • 怎么训练

    对各组中最大的元素来说，输入=输出，即梯度为1；而其他较小的元素则对网络不产生任何影响，同样可以拿掉，从而又可以将网络视为一个瘦长的线性网络。而对不同的输入样本，这种线性关系是不同的，当输入样本很多的时候，网络上的每个参数都能被训练到（这里的理解和ReLU一样）

自适应学习率（Adaptive Learning Rate）

• Adagrad

  $$\boldsymbol{w}^{t+1}\leftarrow\boldsymbol{w}^t-\frac{\eta}{\sqrt{\sum_{i=1}^n(\boldsymbol{g}^i)^2}}\boldsymbol{g}^t$$

  陡峭大学习率，平缓小学习率

  问题：单方向学习率不变

• RMSProp

  $$\boldsymbol{w}^1\leftarrow\boldsymbol{w}^0-\frac{\eta}{\sigma^0}\boldsymbol{g}^0\qquad \sigma^0=\boldsymbol{g}^0\\ \boldsymbol{w}^2\leftarrow\boldsymbol{w}^1-\frac{\eta}{\sigma^1}\boldsymbol{g}^1\qquad \sigma^1=\sqrt{\alpha(\sigma^0)^2+(1-\alpha)(\boldsymbol{g}^1)^2}\\ \boldsymbol{w}^3\leftarrow\boldsymbol{w}^2-\frac{\eta}{\sigma^2}\boldsymbol{g}^2\qquad \sigma^2=\sqrt{\alpha(\sigma^1)^2+(1-\alpha)(\boldsymbol{g}^2)^2}\\ \cdots \\ \boldsymbol{w}^{t+1}\leftarrow\boldsymbol{w}^t-\frac{\eta}{\sigma^t}\boldsymbol{g}^t\qquad \sigma^t=\sqrt{\alpha(\sigma^{t-1})^2+(1-\alpha)(\boldsymbol{g}^t)^2}$$

  虽然同样在算梯度的均方根（Root Mean Square），但可以给新看到的梯度比较大的权重，给过去看到的梯度比较小的梯度，从而解决Adagrad同方向学习率不变的问题。

• Momentum

  除了当前的梯度，还参考了当前的惯性，也就是把之前的梯度也纳入考虑，越远的梯度系数越小，参考影响越小；越近的梯度参考影响越大。这种方法在某些时候可以帮助跳出局部极小值点。

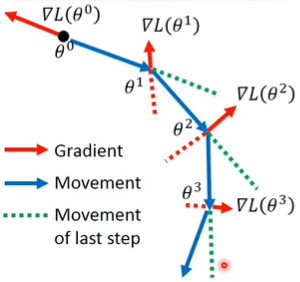
• Adam = RMSprop + Momentum

Bad Results on Testing Data

早点停

正则化 Regularization

重新定义一个损失函数，在原损失函数的基础上加上正则项（以2-norm为例）：

$$L'(\theta)=L(\theta)+\lambda\frac{1}{2}||\theta||_2\\ ||\theta||_2=\sum_{i=1}^n(w_i)^2 \\ \frac{\partial L'}{\partial w}=\frac{\partial L}{\partial w}+\lambda w \\ w^{t+1}\leftarrow w^t-\eta\frac{\partial L'}{\partial w}=(1-\eta\lambda)w^t-\eta\frac{\partial L}{\partial w}$$

正则化一般不考虑 bias 项，因为正则化的目的是让function变得平滑，而bias与function的平滑程度没有关系。

$(1-\eta\lambda)$ 非常接近1，使得 $(1-\eta\lambda)w^t$ 越来越接近0，而后面的微分项保证了整体不会都变成0。

L1和L2的区别：L1的结果很稀疏，会有接近0的点，也会有离0远的点；L2的结果基本都是集中在0附近较小的点

Weight Decay：每次都让weight小一点

目的：参数不要离0太远。（和早点停的作用很像）

Dropout

• 怎么做

  训练时：每次更新参数前，对神经元作采样（包括输入），神经元有p%的几率被丢掉，相连的weight也会相应地被丢掉，所以每次更新时的网络结构都是不同的，并且在训练集上的表现会变差（所以如果训练集本身训练效果就不是很好，就不能加dropout来解决）

  测试时：

  1. 不做dropout
  2. 如果训练时的dropout rate=p%，那么测试的时候，所有weight都要乘上 (1-p%) .

• 为什么有用

  终极Ensemble方法。一个复杂网络往往bias小，但variance很大。通过训练很多个这样的复杂网络，将数据经过所有网络后的输出平均（这与所有weight都乘上(1-p%)等效），这样variance也会得到平均，结果就会比较准。网络越接近线性网络，效果越好。

Backpropagation：反向传播算法

解决的问题：有效计算百万维参数的梯度 $\nabla L(\boldsymbol{\theta})$ <= 更有效的Gradient Desent方法

核心 - 链式法则

$$\frac{\partial L(\boldsymbol{\theta})}{\partial w}=\sum_{i=1}^n\frac{\partial C^n(\boldsymbol{\theta})}{\partial w}\\ z=\boldsymbol{x^i}\boldsymbol{w^i}+b^i=\sum_{j=1}^Nx^i_jw^i_j+b^i$$

根据链式法则：

$$\frac{\partial C}{\partial w}=\frac{\partial C}{\partial z}\frac{\partial z}{\partial w}$$

Forward pass：对所有参数计算$\partial z/\partial{w}$

——-> 其实就是 $w$ 对应的输入

Backward pass：对所有激活函数的输入 $z$ 计算 $\frac{\partial C}{\partial z}$ ，其中 $C$ 表示某一维的Cross Entropy

$$\frac{\partial C}{\partial z}=\frac{\partial C}{\partial a}\frac{\partial a}{\partial z} =\sigma'(z)\Big[w_3\frac{\partial C}{\partial z'}+w_4\frac{\partial C}{\partial z''}\Big]$$

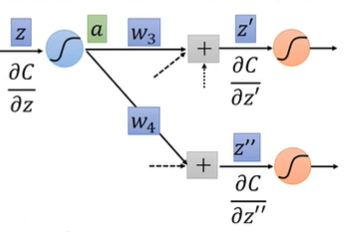
从另一个角度来看，可以把这个式子看作一个反向传播的neuron

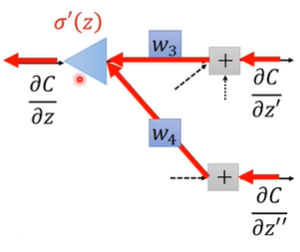
不同的是，在给定 $z$ 的情况下，$\sigma’(z)$ 是个常数，而不是激活函数。

用这种方法就可以从后往前依次算出每个 $z_i$ 的偏微分

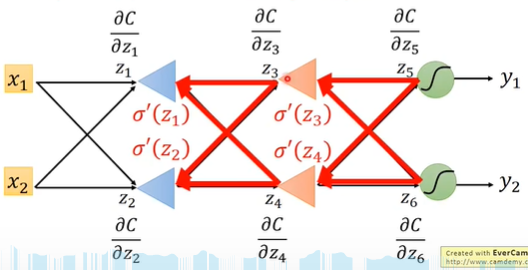
Brief Introduction of Deep Learning

3 steps of Deep Learning

• define a set of function
• goodness of function
• pick the best function

Neural Network

不同的连接方法（logistic regression）形成了不同的网络结构

网络参数 $\boldsymbol{\theta}$ 由所有 logistic regression 各自的weight $\boldsymbol{w}$ 和bias $b$ 组成

如何连接各个logistic regression？

全连接前馈网络 Fully Connect Feedforward Network

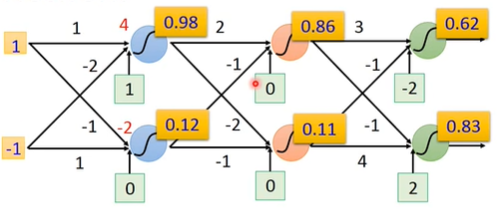
所以可以把一个neural network看成一个function，输入一个vector，输出一个vector：

$$f\Big(\Big[\begin{matrix}1 \\-1 \end{matrix}\Big]\Big)=\Big[\begin{matrix}0 .62\\0.83 \end{matrix}\Big]$$

一个 network structure 即为一个 function set

进一步扩大每一级的neuron个数，得到：

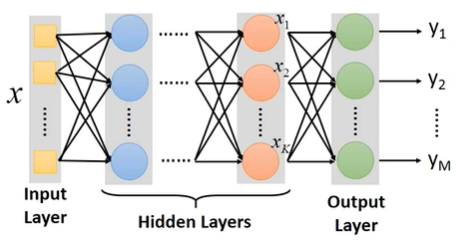
Hidden Layers：代替之前的feature engineering / feature transformation去完成特征提取的工作

Deep：即很多的Hidden Layers

• AlexNet（8层）VGG（19层）GoogleNet（22层）Residual Net（152层）

可以把输出层前一层的 $\boldsymbol{x}^k$ 看作一组变换后的特征向量，这个特征向量可以由一个简单的多分类器（Output Layer）完成分类

用矩阵运算表示网络运作流程

$$\sigma(\boldsymbol{w}^1\boldsymbol{x}+b^1)=\boldsymbol{a}^1\\ \sigma(\boldsymbol{w}^2\boldsymbol{a}^1+b^2)=\boldsymbol{a}^2\\ \cdots\\ \sigma(\boldsymbol{w}^{L}\boldsymbol{a}^{L-1}+b^L)=\boldsymbol{y}$$

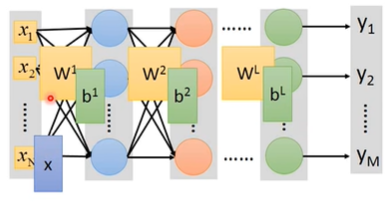
其中的 $\sigma$ 函数就是激活函数

因为把输出层用作一个多分类器，所以最后一层的激活函数应该使用Softmax

写成矩阵运算的好处=>可以用GPU加速

以手写数字识别为例

对一个16 $\times$ 16分辨率的图片来说，网络的输入即为一个256维的向量，输出则为一个10维的向量，每一维代表了这张图片等于0/1/…/9的概率

中间的整个网络结构就相当于定义了一个手写数字识别的 function set，要做的就是用Gradient Descent 去确定这个function的所有参数。在此过程中，需要决定用什么layer，多少layer，每个layer多少neuron，这就决定了function set是否有效。

怎么决定？ 经验和直觉

原来 => 怎么抽取特征。Feature Engineering / Feature Transform，找到一组好的feature

现在 => 怎么设计网络结构。

如何定义一组参数的好坏：依旧Cross Entropy

分类问题用交叉熵

$$C^i=\text{CrossEntropy}(\boldsymbol{y^i},\hat{\boldsymbol{y}}^i)\\ \text{Total_Loss}=\sum_{i=1}^nC^i$$

找到一组参数 $\boldsymbol{\theta}=[w_1,w_2…,b_1,b_2,…]$ 使 Total_Loss 最小（这里把向量 $\boldsymbol{w}$ 都拆开了）

Gradient Descent

1. 给 $\boldsymbol{\theta}$ 随机赋初始值
2. 计算梯度，例如$\frac{\partial L}{\partial {w_1}}$
3. 更新参数，例如$w_1\leftarrow w_1-\mu\frac{\partial L}{\partial {w_1}}$
4. 重复2、3两步，直到梯度小于某一阈值

Backpropagation

一个网络的参数可达百万甚至更多，Backpropagation 是一个比较有效率的计算参数微分（即梯度）的方式

为什么网络越深越好？

• Deep —> Modularization（模组化）类似函数调用

  把一个问题分成几个小问题，分步骤解决。每层网络都能自动从上一层学到更复杂的特征

  在数据量不大的情况下依然能学到较好的表现

  因为没有足够多的数据，所以要deep learning让机器去学习，不然直接查找就好了