潘薇鸿

Multi-class Classification（以三分类为例）

Step 1

Step 2：Softmax计算各分类概率

softmax后所得到的 $y_i$ 满足：$0<y_i<1,\sum_iy_i=1$

why softmax

max仅仅是取最大值，而softmax则是对最大值做了强化。

指数e拉大了数据间的差距，强化大值，换言之，softmax使最大值的辨识度更高。

< softmax的二分类情况就是sigmoid >

Step 3：交叉熵估计分布准确率

将计算所得的 $\boldsymbol{y}=[y_1,y_2, y_3]^T$ 与目标结果 $\hat{\boldsymbol{y}}=[\hat{y_1},\hat{y_2},\hat{y_3}]^T$ 作交叉熵：

其中目标结果 $\hat{\boldsymbol{y}}$ 由one-hot编码表示：

Logistic Regression（以二分类为例）

2021/03/23

Step 1：Function Set

上节得到：

所以我们的函数集即为

此为Logistic Regression ，它与Linear Regression只相差一个 $\sigma$ 函数；Logistic Regression的输出值在0-1之间，而Linear Regression的输出值可以是任何数

Step 2：Goodness of Function

依然是最大似然估计的思想，来估计我们需要的 $\boldsymbol w$ 和 $b$

给定已知数据集的分类，上述函数 $f$ 表示当前数据属于 $C_1$ 的概率，$1-f$ 则表示属于 $C_2$ 的概率（以二分类为例）那么以当前的 $\boldsymbol w$ 和 $b$ 生成该数据集的概率为：

要找 $\boldsymbol w$ 和 $b$ 去最大化这个概率（最大似然估计标准解法，取负对数求导）

但是上面的式子形式非常的不统一，不方便后面的表述，因此对它做一下符号化，即：

那么上面的式子可以被改写为

其实，大括号里的项就是两个伯努利分布的交叉熵（cross entropy)

假设有两个分布 p 和 q，那么他们的交叉熵定义为：$H(p,q)=-\sum_xp(x)ln(q(x))$ ，表示的含义是这两个分布有多接近，即用来衡量两个分布的相似性。如果两个分布完全一样，结果就会是 0。

Logistic Regression: 使用交叉熵判断模型的好坏 - 先验是正态

Linear Regression: 使用误差平方(square error)判断模型好坏 - 先验是二项

Step 3：Find the best function

数学推导！！！

括号内的项表示差距越大，更新越多

但神奇的是

Logistic Regression 的更新方式：

Linear Regression 的更新方式：

其实是一模一样的，唯一不一样的是 $\hat{y}^n$ 和 $f$ 的取值不同

为什么Logistic Regression的损失函数不用Square Error

因为 $f$ 的取值限制在了0-1之间，当估计值和目标距离很远的时候，Square Error的微分值依然很小，非常平坦，更新得很慢

但Cross Entropy在距离目标较远的地方微分值很大，更新得很快

Discriminative(判别模型) v.s. Generative(生成模型)

Discriminative: Logistic Regression => 直接找 $\boldsymbol{w}$ 和 $b$

Generative: 概率模型 => 找 $\boldsymbol{\mu}^1,\boldsymbol{\mu}^2,\boldsymbol{\Sigma}^{-1}$ => 计算 $\boldsymbol{w}$ 和 $b$ （假设了数据分布，这里是高斯分布）

两种方法找出来的w和b会一样么？（不会）=> 同样的模型，不同的方法得到了不同的方程。

生成模型的优势：

• 判别模型的准确率受训练数据量影响大，生成模型的准确率(一般来说)受训练数据量影响小。在训练数据少的情况下，通过假设数据分布提高准确率(但有时候也会适得其反)。

• 假设数据分布的做法，使生成模型对噪声数据更鲁棒

• 生成模型把参数分为 Priors probabilities 和 class-dependent probabilities，可以分别从不同的来源进行估计

  例如语音识别，现在一般使用神经网络实现（Discriminative），但事实上它是个Generative System，DNN只是其中的一部分。对语音识别来说，Priors probability指的是一句话被说出来的概率，这是不需要语音数据的，直接从网上爬文字数据就能计算出某句话出现的概率；class-dependent probability才同时需要语音和文字数据

Logistic Regression的限制

数据必须线性可分才能做。如果不能线性可分，解决方法：Feature Transformation 把原本线性不可分的特征向量转化为线性可分。但并不是所有时候都能知道如何找到一个好的Transformation方法，人找不到，那机器呢？

Cascading Logistic regression models

前两个logistic regression自动完成feature transformation，最后一个logistic regression完成分类

把诸多logistic regression叠加在一起，作进一步推广：

• 某个logistic regression的输入可以是其他logistic regression的输出
• 某个logistic regression的输出可以是其他logistic regression的输入

把每个logistic regression模块叫做一个Neuron，把由logistic regression组成的整体叫做Neural Network

Classification

2021/03/23

为什么不能用regression的方法来处理classification问题：

1. 因为regression模型更在乎整体的Loss是否足够小，这会受到极端error点(“过于正确的点”)的影响
2. 涉及多分类问题，如果把Class i看作输出为i，那么就默认了各个Class之间其实是有联系的（比较接近等），但如果实际上这种关系并不存在的话，就无法得到好的结果

理想的选择

• Function f(x)

  内建函数g(x)，当g(x)>0时，输出class 1；否则输出class 2

• Loss Function L(f)

  训练集上预测错误的次数

  $$L(f)=\sum_n\delta((f(x^n)\neq\hat{y}^n)$$

  但是这个函数是不可微的，所以不能用Gradient Descent解决，而是一般用Perception（感知机），SVM（支持向量机）解决

从概率角度看问题

• 贝叶斯公式

  $$P(C_i|x) = \frac{P(x|C_i)P(C_i)}{\sum_{j=1}^nP(x|C_j)P(C_j)}$$

• Generative Model（生成模型）

  $$P(x)=\sum_{i=1}^nP(x|C_i)P(C_i)$$

• Feature：用一个向量 $\boldsymbol{x}$ 描述个体的特征

• 可以将样本数据（训练集）看作是从一个高斯分布中随机采样得到的，根据样本数据估计高斯分布的均值 $\boldsymbol{\mu}$ 和协方差矩阵 $\boldsymbol{\Sigma}$ ，从而得到该分布的概率密度。找到那个高斯分布，从中选出所有样本数据的概率是最大的，所用的方法就是极大似然估计（Maximum Likelihood）

• 极大似然估计

  $$L(\boldsymbol\mu,\boldsymbol\Sigma)=\prod_{i=1}^nf_{\boldsymbol\mu,\boldsymbol\Sigma}(\boldsymbol x^i) \\\\ \boldsymbol\mu^*,\boldsymbol\Sigma^*=arg\max\limits_{\boldsymbol\mu,\boldsymbol\Sigma}L(\boldsymbol\mu,\boldsymbol\Sigma)$$

  其中的 L 表示极大似然函数，f 表示该分布的概率密度函数。取对数求导求零点：

  $$\boldsymbol\mu^*= \frac{1}{n}\sum_{i=1}^{n}\boldsymbol x^i \\\\ \boldsymbol\Sigma^*=\frac{1}{n}\sum_{i=1}^n(\boldsymbol x^i-\boldsymbol\mu^*)(\boldsymbol x^i-\boldsymbol\mu^*)^T$$

• 存在的问题和解决方法

  因为协方差矩阵的参数很多，当特征函数维度增加时，参数个数会显著增长，从而容易导致过拟合。因此采用共享协方差矩阵的策略，也就是不同分类使用相同的协方差矩阵

  协方差矩阵表示的是特征向量与输出分类之间的线性相关关系，所以可以假设相同。

  又因为可将各分类视为相互独立，所以极大似然函数可改写为（$N$ 个分类，第 $i$ 分类数据个数为 $n_i$ ）：

  $$L(\boldsymbol\mu^1,...,\boldsymbol\mu^N,\boldsymbol\Sigma)=\prod_{i=1}^{n_1}f_{\boldsymbol\mu^1,\boldsymbol\Sigma}(x^i)\prod_{i=1}^{n_2}f_{\boldsymbol\mu^2,\boldsymbol\Sigma}(x^i)...\prod_{i=1}^{n_N}f_{\boldsymbol\mu^N,\boldsymbol\Sigma}(x^i)\\\\ \boldsymbol\mu^{i*}= \frac{1}{n_i}\sum_{i=1}^{n_i}\boldsymbol x^i \\\\ \boldsymbol\Sigma=\sum_{i=1}^N\frac{n_i}{\sum_{j=1}^Nn_j}\boldsymbol\Sigma^i$$

  因为共享协方差矩阵，最后分类的边界会呈线性，把这种模型也叫做线性模型

概率模型的三个步骤

• Function Set (Model) ：基于贝叶斯公式的概率分布
• Goodness of Function：对均值和协方差矩阵的极大似然估计

具体选择哪种概率模型是人为决定的

朴素贝叶斯分类（Naive Bayes Classifier）

前提假设：特征向量的各个维度相互独立（有较强的局限性）

每一项都是一个一维高斯

后验概率 $P(C_1|x)$ 与 sigmoid函数的关系 (假设当前二分类，共用协方差矩阵)

所以最后得到：

所以，何不直接找我们需要的 $\boldsymbol{w}$ 和 $b$ 呢？

New Optimizer for Deep Learning

• 参数更新 $\theta_t = \theta_{t-1} - \eta_{t-1}$

SGD

存在问题：

1. 选择恰当的初始学习率困难

2. 所有参数使用相同的学习率

3. 容易陷入局部极值（导数值为0的局部点）

SGD with Momentum(SGDM)

引入一阶动量 $m_t=\beta \cdot m_{t-1} + (1-\beta)\cdot g_t$ ，$\eta_t=\eta\cdot m_t=\lambda m_{t-1} + \mu g_{t}$

不仅依赖于当前梯度，还依赖于过去的移动（惯性）。坡度陡，惯性大，下降多；坡度缓，惯性小，下降慢

某些时候可以解决陷入局部最小值的情况

Adagrad

分母：陡峭走慢，平缓走快

问题：分母越来越大，最终会导致学习率太小而无法有效更新

RMSProp

主要解决的是Adagrad中，分母太大导致无法有效更新的问题

但依然无法彻底解决

Adam = SGDM + RMSProp

$\theta_t = \theta_{t-1} - \frac{\eta}{\sqrt{\hat{v}_t}+\epsilon}\hat{m}_t$ ($\epsilon=10^{-8}$ ，避免刚开始分母为0)

$\hat{m}_t=\frac{m_t}{1-\beta_1^t}$ （$\beta_1=0.9$）(均值的无偏估计。de-biasing：确保t较小的时候，一阶动量不会因为系数小于1而太小)

$\hat{v}_t=\frac{v_t}{1-\beta_2^t}$ （$\beta_2=0.999$）（方差的无偏估计）

问题：

$\underset{t\rightarrow\infty}{\lim}\frac{\hat{m}_t}{\sqrt{\hat{v}_t}}=1$

这会导致训练很久后，的movement$\rightarrow\eta$​ ，并且不能提供有效的方向信息；而当真正有效的gradient出现时，又会因为前面大量的无效gradient而只产生微不足道的影响

一次更新最多移动的距离不超过$\sqrt{\frac{1}{1-\beta_2}}\eta$

Adam Warm-up

Gradient Descent

gradient：Loss的等高线的法线方向

​ $\left[\begin{array}{cc} \theta_1^1 \\ \theta_2^1 \end{array} \right] = \left[\begin{array}{cc} \theta_1^0 \\ \theta_2^0 \end{array} \right] - \eta \left[\begin{array}{cc} \frac{\partial L(\theta_1^0)}{\partial \theta_1} \\ \frac{\partial L(\theta_2^0)}{\partial \theta_2} \end{array} \right]$ 记作：$\boldsymbol{\theta}^1 =\boldsymbol {\theta}^0-\eta \nabla L(\boldsymbol {\theta}^0)$

1. 小心调整学习率Learning Rate

可视化参数更新次数和Loss的关系，根据这个图，调整学习率

Adaptive Learning Rates 自适应学习率

1. 总原则：通常学习率随着参数的更新越来越小，例如：$\eta^t = \eta/\sqrt{t+1}$

2. 为不同的参数设置不同的学习率，例如Adagrad：$w^{t+1}\leftarrow w^t-\frac{\eta^t}{\sigma^t}g^t$ ，其中 $\sigma^t$ 是个与参数有管的函数，表示过去所有微分值[包括本次]的均方根（RMS：root mean square 所有值的平方求和均值再开方）； $\eta ^t$ 是个与更新次数有关的函数（同上）：

   $$w^{t+1}\leftarrow w^t-\frac{\eta}{\sqrt{\sum_{i=0}^t(g^i)^2}}g^t$$

   分母可以处理梯度突变的情况

   Adam 是现在比较好的更新学习率的方法，训练时间短

3. 在不同参数间比较，需要同时考虑一阶导和二阶导 $\frac{|一阶导数|}{二阶导数}$ ，可以发现Adagrad的分母恰好是二阶导的近似

2. Stochastic Gradient Descent 随机梯度下降

不在全部数据上求loss和，而是选取一个样本计算loss，梯度也只计算这个样本的梯度

比较快

3. Feature Scaling 特征归一化

不归一化的话，各个方向的学习率各有不同，有的方向变化快，学习率就要小一点；有的方向变化慢，学习率就要大一点。

归一化后，各个方向可以使用相同的学习率

一般方法：对某一个维度$i$的数据，求平均值$m_i$和标准方差$\sigma_i$ ，$x^r_i\leftarrow \frac{x^r_i-m_i}{\sigma_i}$

Error来源

1. bias - 距靶心距离（准）
2. variance - 分散程度（稳）

Estimator

• 均值：$m=\frac{1}{N}\sum x^i$ （上标表示第几个变量）
• 均值估计：$E[m]=E\big([\frac{1}{N}\sum x^i]\big)=\frac{1}{N}\sum E[x^i]=\mu$
• 方差：$s^2=\frac{\sigma ^2}{N}=\frac{1}{N}\sum (x^i-m)^2$
• 方差估计：$E[s^2]=E[\frac{1}{N}\sum (x^i-m)^2]=\frac{N-1}{N}\sigma^2\neq\sigma^2$

variance大 - 过拟合

1. 简单模型受训练数据影响小，Variance小；复杂模型Variance大

2. 方法1：增加数据集（效率低，但并不总是practical）- 不会伤害bias

3. 方法2：对损失函数进行正则化（Regularization），平滑曲线 - 会伤害bias

bias大 - 欠拟合

1. 简单模型bias大，复杂模型bias小。<泰勒展开>，模型越复杂，function set越大
2. 说明model本身设计得就不好/过于简单，导致没有包含目标模型，此时收集更多数据是没有用的，需要重新设计model

var增大，bias减小，需要找到平衡点，使得error最小

Model Selection

• Training Set：训练模型

• Validation Set：选模型

• N-fold Cross Validation（N折交叉验证）

  Training Set分成三份，分别作为(train, train, val) (train, val, train) (val, train, train)，模型分别训练三次得到三个error取平均值，选最低error的模型再在整个Training Set上训练一次，得到的结果应用于Testing Set

  不要根据Testing Set调整参数！

Regression

2021/03/22

应用：股票预测系统/自动驾驶/推荐系统

Step1：Model = A set of function

​ Linear Model: $y=b+\sum w_ix_i$ , $w_i$: weight，$b_i$: bias

Step2：Goodness of Function

​ Loss Function $L$ ：input a function, output how bad it is

​ Regularization 正则化：

​ 其中$\lambda$ 是手调的参数，加的一项表示希望参数 $w_i$ 越小越好，越接近0越好

​ 参数值接近0的function是比较平滑的，平滑的函数比较受青睐，因为受输入噪声影响越小；但也不能太平滑。$\lambda$ 越大，考虑平滑越多

​ 做Regularization不考虑bias比较好，bias只是对function上下移动，对平滑程度没有影响

Step3：Best Function

Gradient Descent 梯度下降法

• (随机)选取参数初始值$w^0, b^0$

• 计算初始位置参数对损失函数的（偏）微分（切线斜率）

  • 为负：增大参数

  • 为正：减小参数

  • 步长（Step Size）取决于当前（偏）微分值，和一个常数项（Learning Rate）$\eta$

    $$w^1\leftarrow w^0-\eta\frac{\partial L}{\partial w}|_{w=w^0,b=b^0}$$ $$b^1\leftarrow b^0-\eta\frac{\partial L}{\partial b}|_{w=w^0,b=b^0}$$

  • 重复2、3的步骤，到达局部最小值，但不一定是全局最小值（线性回归没有这个问题）

  • Overfitting 过拟合：减少参量；正则化（Step2）

Introduction

2021/03/22

机器学习：自动找函数

regression + classification + generation

输出数值 二分类/多分类 语句/图像生成

• Supervised Learning：regression/classification（cnn rnn->seq2seq)

  • 提供labeled data，给出正确的输入输出

• 损失函数Loss

  • 自动找出Loss最低的函数

• Reinforcement Learning

  • 不提供输入输出

  • Reward引导机器学习方向

• Unsupervised Leaning：Auto-encoder/GAN

怎么找函数

​ 限定范围：Linear（Regression/Classification) Network Architecture(RNN-seq2seq CNN)

​ 寻找方法：Gradient Descent

Explainable AI

Adversarial Attack 对抗攻击

Network Compression 网络压缩

Anomaly Detection 异常检测：机器如何知道“我不知道”

Transfer Learning 迁移学习

Meta Learning 学习如何学习

Life-Long Learning

卷积神经网络（一）：CNN基本概念

引子：边界检测

在认识卷积神经网络CNN之前，我们先来看一个最简单的例子——边界检测(edge detection)。假设现在有一张6$\times$6的图片：

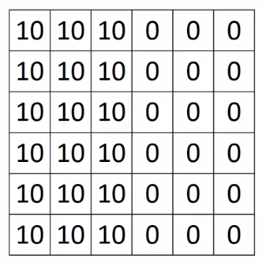
我们都知道，对于一张灰度图，像素值越大，颜色越亮，因此中间两个颜色的分界线就是我们要检测的边界。那么问题来了，怎么检测它呢？我们可以设计这样一个3$\times$3滤波器(filter，或者称为kernel，卷积核)：

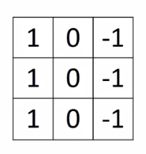
我们拿这个filter去和原来的图片作卷积，也就是当filter覆盖一块相同大小的区域后，将该区域内的元素与自己对应相乘，然后求和，按步长滑动覆盖整个图像，步长的概念后文会解释，下图的例子中步长为1，将得到一个4$\times$4的结果矩阵：

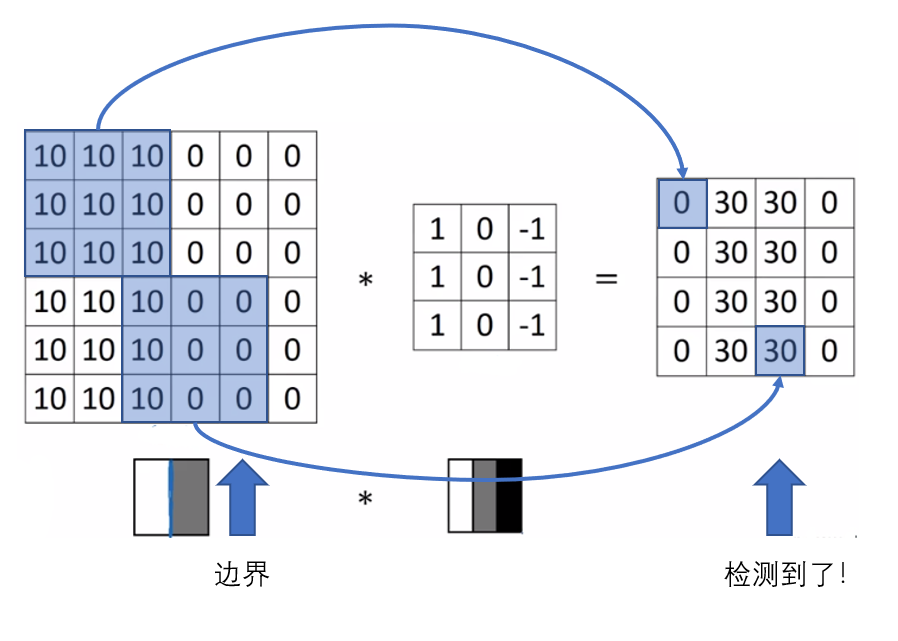
可以发现右边的图中间颜色浅，两边颜色深，说明原图片中间的边界被检测出来了。

上面这个例子说明了，我们可以通过设计特定的filter，让它去和图片作卷积，来识别出图片中的某些特征，例如边界。

上面这个filter用来检测垂直边界，同样的，我们也可以设计出一个检测水平边界的filter，把刚才的filter旋转90$^\circ$即可。对于其他特征，理论上总是可以通过精密的计算检验人工设计出合适的filter，然后CNN(Convolutional Neural Network，卷积神经网络)，就可以通过这一个个不同的filter，不断地提取特征，从局部到整体，从而实现图像识别等工作。

那么问题又来了，对于刚才的图片只是简单的边缘检测，人工设计滤波器可以轻易实现，但是要知道，现实的图片中可能包含了成千上万中特征，想要一一设计出对应的filter，完全不现实。这就到神经网络发挥作用的时候了，这些filter，根本不需要我们去设计，只需要将每个filter中的各个数字看作一个参数，让机器通过大量的数据自己去学习它们就可以了，甚至还可以实现比人工计算更加合适的滤波器。

以上就是CNN的基本原理。

CNN的基本概念

Padding

为了构建卷积神经网络，Padding是一个基本的卷积操作。从上面的例子中我们发现，一个6$\times$6的图像经过3$\times$3的filter卷积之后变小了(4$\times$4)，更普通地说，一个$n\times n$的图像，用一个$f\times f$的滤波器做卷积，得到的图像大小将变为$(n-f+1)\times (n-f+1)$，这样就会产生两个问题：

• 每做一次卷积图像就会缩小一次，这样没几次卷积图像就没了，尤其对于深度神经网络而言，是不希望发生的；
• 相较图像中心的点而言，边缘像素点在卷积中计算的次数很少，容易丢失边缘信息。

针对这两个问题的解决方法是，在每次做卷积之前，填充整个图像使得卷积后的图像大小和原始图像大小相同，同时，原图的边缘也能参与更多次的计算。通常，填充的像素值都为0。

参数p用来指定在原图周围填充的像素圈数，例如在上面的例子中，我们指定p=1，那么原来6$\times$6的图像的周围将多出一圈像素值为0的像素，从而变成一个8$\times$8的图像，在经过3$\times$3的filter后，得到的结果将是一个6$\times$6的图像，和原图一样大，没有缩小。

Padding常用的有两种方式：

• Valid: p=0，即不经过任何像素填充；
• Same: 让卷积之后的图像大小不变的Padding方式

当我们使用Same方式时，如何计算参数p的具体值呢？假设我们现在有一个$n\times n$的图像，和一个$f\times f$的滤波器，在原图周围填充p圈像素后得到的图像大小为$(n+2p)\times (n+2p)$，那么卷积后得到的图像大小为$(n+2p-f+1)\times (n+2p-f+1)$，要使它和原图大小相等，则必须$n=n+2p-f+1$，从而得到$p=\frac{f-1}{2}$。

习惯上，在计算机视觉中，$f$通常是奇数，很少见到一个偶数的滤波器。

Stride

Stride(步长)是构建卷积神经网络的另一个基本操作，它决定了卷积核每次移动过几行/列像素，以下面7$\times$7图像卷积3$\times$3filter为例，可以清楚地了解Stride的作用：

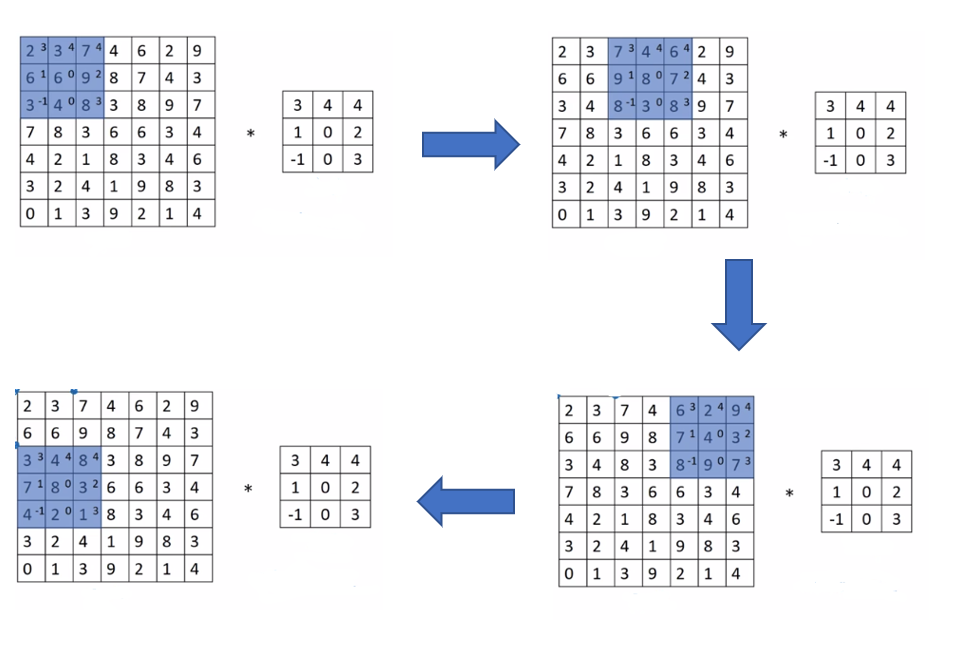
卷积得到的图像大小由下面这个公式给出：

当无法整除时向下取整，它的实际意义是，只有当filter完全在被卷积图像中时才能进行卷积操作。

Pooling

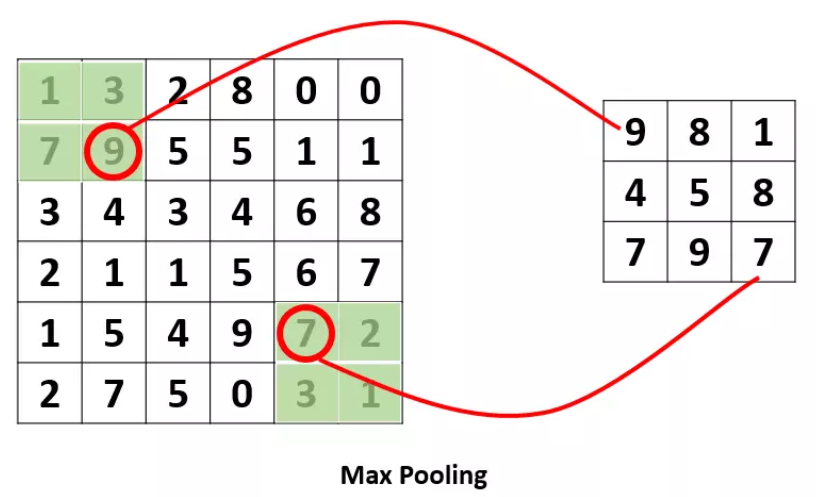
Pooling操作是为了提取一定区域内的主要特征，并减少参数的数量，防止模型过拟合，例如下面的Max Pooling，它采用了一个2$\times$2的窗口，步长为2，其作用是取每个2$\times$2的窗口中的最大值，构成最终的输出。

多通道(channels)图像卷积

我们在日常生活中所接触的图像通常是RGB图像，即除了长宽外，它还有RGB三个通道(channel)，因此输入卷积神经网络的数据也不再是简单的长$\times$宽，而应该是长$\times$宽$\times$通道。那么相对应的，我们的filter也要从二维变化成三维，沿用上面的例子，filter的维度就要变成(3,3,3)，其最后一维必须和输入的channel维度一致。

这时候的卷积运算，是三个channel的所有元素对应相乘后求和，换言之，之前是九个乘积的和，而现在则是27个乘积的和，因此输出图像的维度并不会发生变化，还是和二维时的一样。

但一般情况下，我们会使用多个filter来检测多个不同的特征，每个filter的输出对应最终输出图像的一层，例如上面的例子中，我们采用了4个不同的滤波器，假设分别是垂直边缘滤波器，水平边缘滤波器，45$^{\circ}$边缘滤波器，75$^{\circ}$边缘滤波器，那么输出图像维度将会是(4,4,4)，最后一维取决于使用的滤波器个数，每一层图像对应了一个不同的特征。

单层卷积神经网络

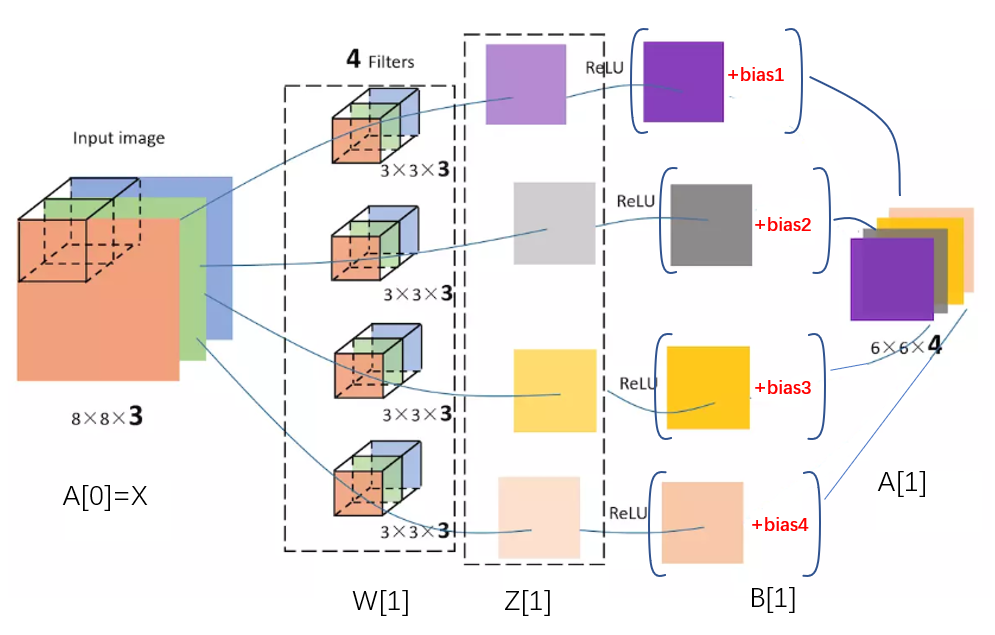
对卷积得到的输出图像加上偏置并由激活函数激活后，我们最终得到了第一层的输出，亦即第二层的输入：

CNN的组成结构

CNN包含了三种层

卷积层(Convolutional layer — CONV)

上面介绍的所有内容都是卷积层相关的，它由滤波器filter和激活函数构成，设计卷积层时涉及的超参数包括：filter的数量、大小、步长、是否填充、填充大小、偏差，以及激活函数的选择。

池化层(Pooling layer — POOL)

除了卷积层，卷积网络也经常使用池化层来缩小模型的大小，提高计算速度，同时提高所提取的特征的鲁棒性。

最常用的算法是Max Pooling，这在上文也提到过。最大化操作的功能是，只要在任何窗口内提取到某个特征，它都会保留在最大池化的输出里，换言之，如果在过滤器中提取到了某个特征，那么保留其最大值；如果没有提取到这个特征，那么这块区域中不存在这个特征，其中的最大值也还是很小。

另外还有一种不太常用的池化方法——平均池化(Average Pooling)，顾名思义，它不取最大值而是计算平均值。

池化的超参数包括窗口大小$f$，步长$s$，以及池化方式。常用参数值为$f=2,s=2$，其效果相当于高度和宽度各减少一半，也有使用$f=3,s=2$的情况。池化层没有需要学习的超参数。

全连接层(Fully Connected layer —FC)

这就是我们之前学的神经网络中的最普通的层，就是一排神经元。因为这一层是每一个单元都和前一层的每一个单元相连接，所以称之为“全连接”。这里要指定的超参数无非就是神经元的数量，以及激活函数。

一个CNN的典型架构

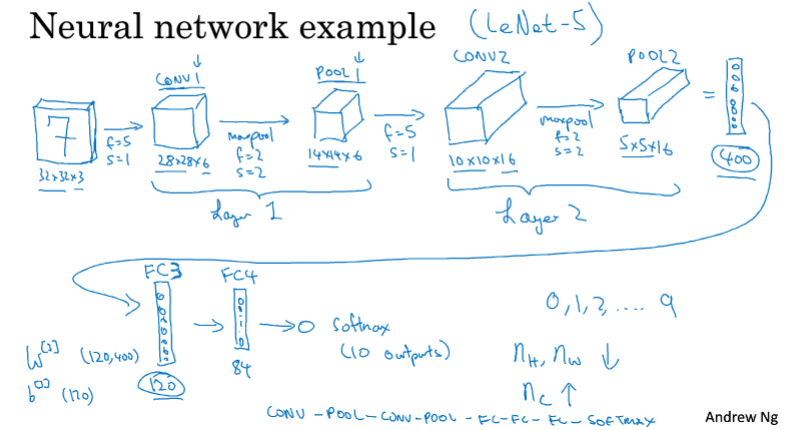
如上图，对一个输入的(32,32,3)的手写数字图像，经过第一次卷积(f=5,s=1,p=0,n=6,ReLU)，得到(28,28,6)的CONV1，再经由最大池化层(f=2,s=2)得到(14,14,6)的POOL1，通常我们将CONV1和POOL1合称为Layer1。然后再过一次(f=5,s=1,p=0,n=16,ReLU)的卷积，得到(10,10,16)的CONV2，经过最大池化层得到(5,5,16)的POOL2，将POOL2展开(扁平化)即得到一个长为400的向量，后面的操作就与一般神经网络无异了(经过两个全连接层后变成长为84的向量，作为Softmax的输入)。

CONV(relu)-POOL-CONV(relu)-POOL-FC-FC-FC-Softmax

以上就是一个典型的CNN架构，在这个过程中我们可以发现，随着网络的深入，图像的长宽在不断减小，而通道数(深度)在不断增加。

OpenCV实现仿射变换

OpenCV实现仿射变换涉及两个主要函数——gerRotationMatrix2D和warpAffine，前者可以根据旋转角度，缩放因子等获得旋转矩阵，后者可以根据已知的变换矩阵实现一些简单的重映射。

cv::getRotationMatrix2D函数

函数原型

1
2
3
4
5

cv::Mat cv::getRotationMatrix2D(
    Point2f center,
    double  angle,
    double  scale
)

• center: 原图像的旋转中心
• angle: 图像旋转角度，正逆负顺
• scale: 缩放系数

cv::warpAffine函数

函数原型

1
2
3
4
5
6
7
8
9

void cv::warpAffine(
    InputArray    src,
    OutputArray   dst,
    InputArray    M,
    Size          dsize,
    int           flags = INTER_LINEAR,
    int           borderMode = BORDER_CONSTANT,
    const Scalar& borderValue = Scalar()
)

• src: 输入图像
• dst: 输出图像
• M: 2$\times$3的变换矩阵
• dsize: 图像输出尺寸
• flags: 插值算法标识符，默认值为INTER_LINEAR，常用插值算法如下
  • INTER_NEAREST: 最临近插值算法
  • INTER_LINEAR: 线性插值算法
  • INTER_CUBIC: 双立方插值算法
  • INTER_AREA: 区域插值算法（使用像素区域关系的重采样时图像抽取的首选方法，但是当图像被放大，它类似于INTER_NEAREST方法）
  • INTER_LANCZOS4: Lanczos插值（超过8$\times$8邻域的插值算法
  • INTER_MAX: 用于插值的掩模版
  • WARP_FILL_OUTLIERS: 标志位，用于填充目标图像的像素值，如果其中的一些值对应于原图像中的异常值，那么这些值将被设置为0
  • WARP_INVERSE_MAP: 标志位，反变换
• borderMode: 边界像素模式，默认值为BORDER_CONSTANT
• borderValue: 边界取值，有默认值为Scalar()，即为0

图像翻转 - cv::flip(InputArray src, OutputArray dst, int flipCode)

• src: 输入矩阵
• dst: 翻转后矩阵，类型与src一致
• flipCode: 翻转模式，flipCode==0垂直翻转（沿X轴翻转），flipCode>0水平翻转（沿Y轴翻转），flipCode<0水平垂直翻转（先沿X轴翻转，再沿Y轴翻转，等价于旋转180°）

cv::Mat重载运算符operate()

函数原型

1
2
3
4

inline Mat Mat::operator()( Range _rowRange, Range _colRange ) const
{
    return Mat(*this, _rowRange, _colRange);
}

除了分别传入行列的范围外，还可以直接传入cv::Rect类来截取图像中的指定区域。

1
2
3
4
5

cv::Mat img, target_img;
cv::Point2f center;
int width, height;
cv::Rect target = cv::Rect(center.x, center.y, width, height);
target_img = img(target);

如何截取旋转矩形内的图像

由于旋转矩形不是常规矩形（与轴平行），所以首先要将图像作旋转变化，旋转中心即为旋转矩形中心，使得旋转矩形内部的图像在窗口中是与坐标轴平行的，然后从旋转矩阵得到一般矩阵，通过cv::Mat的重载运算符operate()得到局部图像。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

   //const cv::Mat &image, const cv::RotatedRect &rect
cv::Point2f vertex[4];
   
rect.points(vertex);
auto center = rect.center;
cv::Mat rot_mat = cv::getRotationMatrix2D(rect.center, rect.angle, 1);
cv::Mat rot_image;
cv::Mat roi_image;
warpAffine(image, rot_image, rot_mat, rot_image.size(), INTER_LINEAR, BORDER_CONSTANT);  // warpAffine use 2ms
cv::Rect target = cv::Rect(center.x - (rect.size.width / 2),
						   center.y - (rect.size.height / 2),
						   rect.size.width, rect.size.height);
if (makeRectSafe(target, image.size()) == true)
{
	roi_image = rot_image(target);
	cv::resize(roi_image, roi_image, cv::Size(80, 60));
	char str[100];
	sprintf_s(str, "D:\\theThirdYear\\RM\\task1\\number\\%d.jpg", img_idx++);
	cv::imwrite(str, roi_image);
}

其中用到的函数是用来保证target矩形是正常的，否则可能会报错。

1
2
3
4
5
6
7
8
9
10
11
12
13

bool makeRectSafe(cv::Rect & rect, cv::Size size) {
	if (rect.x < 0)
		rect.x = 0;
	if (rect.x + rect.width > size.width)
		rect.width = size.width - rect.x;
	if (rect.y < 0)
		rect.y = 0;
	if (rect.y + rect.height > size.height)
		rect.height = size.height - rect.y;
	if (rect.width <= 0 || rect.height <= 0)
		return false;
	return true;
}